Antes de seguir con el repaso a los algoritmos, me parece imprescindible mencionar un artículo que descubrí gracias a este tweet de @jjcanido:
Se trata de un artículo de Stuart Plunkett, del año ¡1979! No lo conocía, y me ha parecido una de las exposiciones más claras y convincentes que conozco sobre la obsolescencia de los algoritmos tradicionales, y la conveniencia de otro tipo de algoritmos que favorezcan la comprensión.
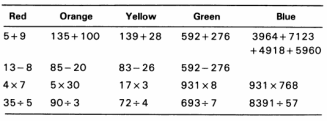
Una de las cosas que lo hace interesante es que se atreve con algo que muchas veces echo en falta en este tipo de propuestas, y es concretar qué tipo de cálculos habría que hacer de qué manera. Lo resume en esta tabla:
La columna Red corresponde a los «hechos básicos», que deben estar (a partir de cierta edad, claro) accesibles en memoria para facilitar cálculos más avanzados. La columna Orange corresponde a cálculos que se reducen a un solo paso que usa los hechos de la columna anterior. Para estos cálculos, los algoritmos tradicionales son absolutamente inapropiados. La columna Yellow corresponde a cálculos para los que las técnicas «mentales» son idóneas. Plunkett afirma que cualquier persona podría hacerlos mentalmente, si lo necesitara (me temo que aquí Plunkett es optimista, o las cosas han empeorado bastante, seguramente por culpa de la enseñanza de la aritmética en la escuela). Están también perfectamente al alcance de un alumno de la segunda mitad de primaria, con el trabajo adecuado. Los cálculos de la columna Green se podrían hacer mentalmente, pero poca gente lo necesitará. Por último, para los cálculos de la columna Blue sería absurdo recurrir a las técnicas del cálculo mental, igual de absurdo que recurrir al lápiz y al papel si tenemos a mano una calculadora (el énfasis es mío).
Creo que merecería la pena tratar de difundir artículos como este entre la comunidad de docentes. En particular, entre los maestros de educación primaria. Si algún lector tiene contactos con alguna revista para ese sector que pudiera estar interesada, o conoce una versión en castellano de este trabajo, le agradecería que se pusiera en contacto conmigo, por ejemplo a través de los comentarios.
Actualización (24/09/2017). Juan Emilio García me ha hecho llegar esta traducción del artículo. ¡Muchas gracias!
Después de estos párrafos iniciales puede parecer un poco absurdo volver al repaso de los algoritmos tradicionales. Sin embargo, vistos los progresos de estos últimos 40 años, creo que merece la pena tratar de dar pequeños pasos en la dirección de hacer la «aritmética del lápiz y papel» un poco más «pensada».
La multiplicación:
La propiedad clave que permite multiplicar números grandes a partir de las tablas de multiplicar es la propiedad distributiva. Por tanto, si nuestro objetivo es elegir un algoritmo que ayude a la comprensión, el objetivo debe ser considerar algoritmos en los que sea sencillo ver cómo aplicamos la propiedad distributiva.
Antes de tratar de formalizar ningún tipo de algoritmo para la multiplicación, debería estar claro que 
Una vez entendida la propiedad distributiva, escribir este cálculo en el formato que se muestra a la izquierda en la figura me parece inmediato. Es verdad que, si queremos (o nos obligan a) tratar multiplicadores de más de una cifra, habría que pasar a la escritura tradicional, de la derecha. 
La escritura de la multiplicación con multiplicadores de más de una cifra es uno de los puntos más problemáticos si queremos insistir en una escritura de los algoritmos que ayude a la comprensión. Quizá lo mejor sería escribir que 37 veces 25 son 30 veces 25 más 7 veces 25, y a partir de ahí hacer los cálculos correspondientes. Evidentemente, estoy hablando de cómo escribir los algoritmos cuando se están aprendiendo. Si es necesario o no llegar a una escritura refinada al final del proceso, o si esto no merece la pena, es algo que se escapa del objetivo de esta entrada. Lo que sí tengo claro es que, incluso en la escritura tradicional del algoritmo, no deberíamos dejar el hueco de las unidades al multiplicar por las decenas, sino poner el número que ocupa ese lugar, que es el cero, claro. Es uno de esos detalles donde los usos y costumbres presentes en nuestras aulas (y en nuestros libros de texto) chocan de manera para mi incomprensible con la didáctica.
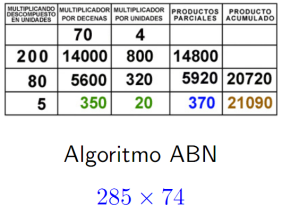
En la siguiente figura se muestra la tabla que usan los algoritmos ABN para calcular 
Por último, le llega el turno a la división. Sobre el algoritmo tradicional, quiero insistir una vez más en lo poco conveniente que me parece dejar de escribir las restas y calcularlas mentalmente. Es un detalle que hace que el algoritmo sea más difícil de ejecutar, más complicado de entender, y que lo desconecta de variantes como la división de polinomios en secundaria. Por lo que voy averiguando parece que en el pasado lo usual en nuestro país era aprender primero poniendo las restas, para eliminarlas más adelante. Poco a poco, ese momento de eliminar las restas parece haberse ido adelantando, y en muchas ocasiones los alumnos aprenden directamente el algoritmo de la división restando mentalmente. Me parece un ejemplo perfecto donde se aplica esta cita de Donald Knuth «Premature optimization is the root of all evil (or at least most of it) in programming» que enunció pensando en la programación, pero que me parece perfectamente trasladable al aprendizaje de las matemáticas. En la figura vemos un ejemplo tomado de un libro de texto de 3º de Primaria.
En este tema solo nos siguen algunos países hispanoamericanos. Si revisamos vídeos de alumnos haciendo divisiones en Gran Bretaña, Francia, o Alemania, podemos ver que hay variaciones en cómo organizan los cálculos, pero que tienen una cosa en común: escriben las restas.
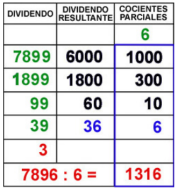
No me convence la forma de organizar los cálculos de la división ABN (en la imagen de la derecha se puede ver un ejemplo), pero la idea sí es natural, y explicando el pasado septiembre el algoritmo ABN en magisterio se me ocurrió que un buen algoritmo para la división sería la mezcla del tradicional y la idea de los ABN que muestro en la siguiente figura. Es un algoritmo donde se trabaja la descomposición de los números, y que cada niño puede aplicar adaptándolo a su nivel de cálculo. Naturalmente, la idea no es nueva, y posteriormente descubrí que aparece en la literatura como «división de Brousseau», y Cecilia Calvo y David Barba hablaron de él en un número reciente de la revista SUMA (que no he podido localizar en una búsqueda rápida. Cierro con una pequeña petición para los editores de la revista: sería muy útil que los índices estuvieran accesibles online).
Más ideas, menos cuentas. Un blog sobre educación matemática. 
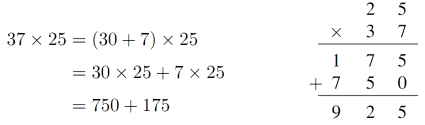
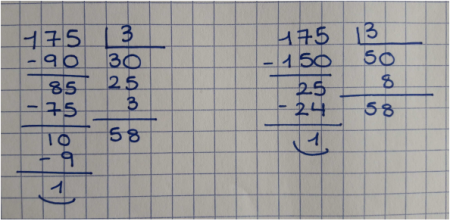
Tu propuesta de división es conocida como «división por cocientes parciales» en el currículo norteamericano: Partial Quotiens Division (aquí puedes ver cómo un par de explicaciones :https://goo.gl/KvkkRE (Khan Academy) o Everyday Maths de la Universidad de Chicago (https://goo.gl/5vV75R) y en ambos casos utilizan el significado de división quotativa o de medida que aquí tantas veces omitimos.
El índice de la revista SUMA puedes consultarlo, desde el número 54 hasta el último que he recibido (84), en el siguiente enlace de elaboración propia:
https://docs.google.com/spreadsheets/d/112QDRnbt-EpoYVt7d875x9lMLKffySfV01lQXlxQZz0/edit?usp=sharing
Complementando lo que apunta cadoi, en su blog PuntMat mantienen un índice de publicaciones, que incorpora los artículos de Suma(con el texto completo en Google Drive):
http://puntmat.blogspot.com.es/p/publicacions.html
Muchas gracias a los dos. Ahí está, en efecto. El número de SUMA es el de noviembre de 2016.
Como siempre, excelentes los artículos, enhorabuena 🙂
Me gustaría comentar un par de cosas curiosas con respecto al algoritmo de la multiplicación.
En el último capítulo de Aprender de grandes, Andrés Rieznik, mago argentino que ha sido ponente varias veces en las TED Talks (https://soundcloud.com/aprenderdegrandes/andres2, minuto 13:20), comentaba que el orden en que se hace la multiplicación importa a la hora de computar el tiempo cerebral.
Técnicamente se denomina «efecto orden», sigue la estructura máximo-mínimo, parece depender de la lejanía de los números y es extensible a la suma (donde 6+2 es mentalmente más rápido de realizar que 2+6) Esto no ocurre con números cercanos, como 3×2.
Ejemplo: 3×7 vs 7×3. De la primera forma se tardaría, en promedio, unos 50 milisegundos más que de la segunda. Rieznik lo atribuye al significado semántico: 7 veces 3 parece ser muy diferente – a nivel cerebral – que 3 veces 7, puesto que (según él), el cerebro realizaría 7x7x7 en lugar de 3x3x3x3…
Los resultados fueron tomados de la aplicación para Android llamada Moravec(para desarrollar el cálculo «ágil» al hacer cuentas).
El estudio es: Arithmetic on Your Phone: A Large Scale Investigation of Simple Additions and Multiplications http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0168431. En el estudio «colaboran» pesos pesados de la neurociencia como Dehaene y Sigman.
Lo que me ha recordado tus vídeos es la posible [gran] importancia de emplear el término «veces», en lugar de «por», que carecería de «significado» para el niño. Rieznik lo comenta, unido a lo siguiente: ¿sucedería lo mismo en un país anglosajón? En Reino Unido, por ejemplo, dicen 7 «times» 3… Pero, claro, entonces sucedería a la inversa, puesto que para ellos esto significa «7 veces 3», lo que les llevaría a 3x3x3x3… En el momento del programa, con unos 10.000 datos recogidos, parecía que iba a ser así, pero aún no era significativo.
Por otro lado, versiones de la multiplicación donde entra en juego una «rima» auditiva, podían acelerar el resultado hasta en 300 milisegundos (en promedio). Por ejemplo, 7×5 «treinta y cinco» – es lo que pensamos mentalmente – es mucho más veloz que 5×7, que carece de rima asociada. Lo mismo sucede con 6×4, 6×8, etc.
Otro tema: los «trucos» para realizar operaciones más ágilmente. Lo has citado de algún vídeo norteamericano, creo que decías (lo relaciono con lo que viene en el siguiente párrafo, pero igual me equivoco). Siempre con cuidado de no perder el «por qué» y «de dónde viene» – el significado por el que tanto abogas, y con mucha razón, como restar en las divisiones o contar con los dedos -. Vaya , que adaptar algunos trucos de las personas que realizan tales operaciones rápidamente podría ser muy interesante. Ejemplo: multiplicar o elevar al cuadrado es coser y cantar, si bien en este último caso habría que transmitir el porqué.
En concreto, hay algo que para los «maestros de la memoria» tiende a ser natural y prácticamente necesario: realizar sumas, multiplicaciones, etc, de izquierda a derecha. La verdad, dado que pensamos de ese modo (escribimos así, etc), y lo sencillo que viene a ser (sin perder significado), casi creo es una pena que no se haga así. Por eso antes he dicho «prácticamente necesario», ya que no sé qué ocurre con los hablantes árabes que realizan tales cálculos.
Ya para terminar, Arthur Benjamin, uno de los introductores de la magia unida a las matemáticas (la matemagia, que puede enganchar bastante a los chicos) comentaba algo que probablemente también es esencial, y que meimagino que debatiréis día sí y día también 🙂
Decía (https://www.ted.com/talks/arthur_benjamin_s_formula_for_changing_math_education?language=es) que en lugar de estar el cálculo en la cima de la pirámide deberían estar la probabilidad y la estadística. Algo fundamental para el día a día – él habla salteadamente de «riesgo, recompensa, aleatoriedad, analizar tendencias, predecir el futuro…». Claro que ahí no habla de las edades de los niños, pero de alguna manera creo que todos sentimos que los tiros deberían ir más por esa parte. Otro tema es el margen que os dan para maniobrar.
De nuevo, gracias a todos (autor y comentaristas), por este excelente blog.
Un cordial saludo
Muchas gracias por tu comentario, Jorge.
Y gracias por la referencia a ese artículo sobre análisis del cálculo usando los móviles. Lo miraré en cuanto pueda.
Un comentario: no sé si analizan la relación entre rapidez de respuesta y facilidad de comprensión. Puede no ser exactamente lo mismo …
Sí conocía los vídeos y las propuestas de Arthur Benjamin. En efecto, muy interesantes.
Acabo de ver este vídeo de James Tanton sobre «the area model» para multiplicación, que yo he usado en álgebra:
Aquí un vídeo de este método de cajas para la división:
Este me convence bastante menos. Claro que no te sabes la tabla del 15, pero saber cuántas son 15 x 10, de hecho, 15 x 20, me parece un prerrequisito para empezar con la división con divisores de dos cifras.
Muchas gracias por aportar el enlace, Juan José. Sí, vi el vídeo hace un par de días, y creo que hace un trabajo estupendo sobre todo en mostrar como la idea de conectar la multiplicación con el área puede ayudar después para otras cosas distintas. Ya hace un par de cursos que introduje el modelo de áreas en magisterio, y tengo claro que es «la forma» de entender mejor la multiplicación. (A pesar de que a los alumnos les cuesta muchísimo empezar a dibujar).
Hola, Pedro!! Muchas gracias por tener en cuenta nuestro trabajo.
El número de la revista SUMA donde seguramente hayas leído nuestro comentario sobre el algoritmo de la división es el nº83. En el blog del PuntMat están disponibles los títulos de las entregas de la sección «Ell@s tienen la palabra» y acceso directo al pdf de cada una: https://puntmat.blogspot.com/p/publicacions.html
Muchas gracias por el enlace, Cecilia.
Pingback: Jornada en el CTIF Madrid-Este | Más ideas, menos cuentas. Un blog sobre educación matemática.
Pingback: España lleva décadas suspendiendo en matemáticas. La ciencia tiene claro cómo podemos arreglarlo
Pingback: España lleva décadas suspendiendo en matemáticas. La ciencia tiene claro cómo podemos arreglarlo – Tecnologías de información del golfo
Pingback: España lleva décadas suspendiendo en matemáticas. La ciencia tiene claro cómo podemos arreglarlo - Radio Onda Digital
Pingback: Xataka – España lleva décadas suspendiendo en matemáticas. La ciencia tiene claro cómo podemos arreglarlo – Yacal