Antes de seguir con el repaso a los algoritmos, me parece imprescindible mencionar un artículo que descubrí gracias a este tweet de @jjcanido:

Se trata de un artículo de Stuart Plunkett, del año ¡1979! No lo conocía, y me ha parecido una de las exposiciones más claras y convincentes que conozco sobre la obsolescencia de los algoritmos tradicionales, y la conveniencia de otro tipo de algoritmos que favorezcan la comprensión.

Una de las cosas que lo hace interesante es que se atreve con algo que muchas veces echo en falta en este tipo de propuestas, y es concretar qué tipo de cálculos habría que hacer de qué manera. Lo resume en esta tabla:

La columna Red corresponde a los «hechos básicos», que deben estar (a partir de cierta edad, claro) accesibles en memoria para facilitar cálculos más avanzados. La columna Orange corresponde a cálculos que se reducen a un solo paso que usa los hechos de la columna anterior. Para estos cálculos, los algoritmos tradicionales son absolutamente inapropiados. La columna Yellow corresponde a cálculos para los que las técnicas «mentales» son idóneas. Plunkett afirma que cualquier persona podría hacerlos mentalmente, si lo necesitara (me temo que aquí Plunkett es optimista, o las cosas han empeorado bastante, seguramente por culpa de la enseñanza de la aritmética en la escuela). Están también perfectamente al alcance de un alumno de la segunda mitad de primaria, con el trabajo adecuado. Los cálculos de la columna Green se podrían hacer mentalmente, pero poca gente lo necesitará. Por último, para los cálculos de la columna Blue sería absurdo recurrir a las técnicas del cálculo mental, igual de absurdo que recurrir al lápiz y al papel si tenemos a mano una calculadora (el énfasis es mío). 

Creo que merecería la pena tratar de difundir artículos como este entre la comunidad de docentes. En particular, entre los maestros de educación primaria. Si algún lector tiene contactos con alguna revista para ese sector que pudiera estar interesada, o conoce una versión en castellano de este trabajo, le agradecería que se pusiera en contacto conmigo, por ejemplo a través de los comentarios.

Actualización (24/09/2017). Juan Emilio García me ha hecho llegar esta traducción del artículo. ¡Muchas gracias!

Después de estos párrafos iniciales puede parecer un poco absurdo volver al repaso de los algoritmos tradicionales. Sin embargo, vistos los progresos de estos últimos 40 años, creo que merece la pena tratar de dar pequeños pasos en la dirección de hacer la «aritmética del lápiz y papel» un poco más «pensada».

La multiplicación:

La propiedad clave que permite multiplicar números grandes a partir de las tablas de multiplicar es la propiedad distributiva. Por tanto, si nuestro objetivo es elegir un algoritmo que ayude a la comprensión, el objetivo debe ser considerar algoritmos en los que sea sencillo ver cómo aplicamos la propiedad distributiva.

Antes de tratar de formalizar ningún tipo de algoritmo para la multiplicación, debería estar claro que , es decir que «7 veces 25 son 7 veces 20 más 7 veces 5». Creo que en este punto el uso de «veces» en lugar de «multiplicado por» supone una gran ventaja. Representaciones gráficas como las de la figura ayudan a entender el significado de la propiedad distributiva. La versión de la derecha, sin las unidades representadas explícitamente, supone un paso más en el nivel de abstracción.

Una vez entendida la propiedad distributiva, escribir este cálculo en el formato que se muestra a la izquierda en la figura me parece inmediato. Es verdad que, si queremos (o nos obligan a) tratar multiplicadores de más de una cifra, habría que pasar a la escritura tradicional, de la derecha. 

La escritura de la multiplicación con multiplicadores de más de una cifra es uno de los puntos más problemáticos si queremos insistir en una escritura de los algoritmos que ayude a la comprensión. Quizá lo mejor sería escribir que 37 veces 25 son 30 veces 25 más 7 veces 25, y a partir de ahí hacer los cálculos correspondientes. Evidentemente, estoy hablando de cómo escribir los algoritmos cuando se están aprendiendo. Si es necesario o no llegar a una escritura refinada al final del proceso, o si esto no merece la pena, es algo que se escapa del objetivo de esta entrada. Lo que sí tengo claro es que, incluso en la escritura tradicional del algoritmo, no deberíamos dejar el hueco de las unidades al multiplicar por las decenas, sino poner el número que ocupa ese lugar, que es el cero, claro. Es uno de esos detalles donde los usos y costumbres presentes en nuestras aulas (y en nuestros libros de texto) chocan de manera para mi incomprensible con la didáctica.

En la siguiente figura se muestra la tabla que usan los algoritmos ABN para calcular . No me parece que ayude a la comprensión. Como ocurre muchas veces con los procedimientos que llevan a tablas, creo que más bien promueve la mecanización sin reflexión.

Por último, le llega el turno a la división. Sobre el algoritmo tradicional, quiero insistir una vez más en lo poco conveniente que me parece dejar de escribir las restas y calcularlas mentalmente. Es un detalle que hace que el algoritmo sea más difícil de ejecutar, más complicado de entender, y que lo desconecta de variantes como la división de polinomios en secundaria. Por lo que voy averiguando parece que en el pasado lo usual en nuestro país era aprender primero poniendo las restas, para eliminarlas más adelante. Poco a poco, ese momento de eliminar las restas parece haberse ido adelantando, y en muchas ocasiones los alumnos aprenden directamente el algoritmo de la división restando mentalmente. Me parece un ejemplo perfecto donde se aplica esta cita de Donald Knuth «Premature optimization is the root of all evil (or at least most of it) in programming» que enunció pensando en la programación, pero que me parece perfectamente trasladable al aprendizaje de las matemáticas. En la figura vemos un ejemplo tomado de un libro de texto de 3º de Primaria.

En este tema solo nos siguen algunos países hispanoamericanos. Si revisamos vídeos de alumnos haciendo divisiones en Gran Bretaña, Francia, o Alemania, podemos ver que hay variaciones en cómo organizan los cálculos, pero que tienen una cosa en común: escriben las restas.

No me convence la forma de organizar los cálculos de la división ABN (en la imagen de la derecha se puede ver un ejemplo), pero la idea sí es natural, y explicando el pasado septiembre el algoritmo ABN en magisterio se me ocurrió que un buen algoritmo para la división sería la mezcla del tradicional y la idea de los ABN que muestro en la siguiente figura. Es un algoritmo donde se trabaja la descomposición de los números, y que cada niño puede aplicar adaptándolo a su nivel de cálculo. Naturalmente, la idea no es nueva, y posteriormente descubrí que aparece en la literatura como «división de Brousseau», y Cecilia Calvo y David Barba hablaron de él en un número reciente de la revista SUMA (que no he podido localizar en una búsqueda rápida. Cierro con una pequeña petición para los editores de la revista: sería muy útil que los índices estuvieran accesibles online).

Este curso he repensado bastante la asignatura de Aritmética (para maestros) y he dedicado cierto tiempo a pensar sobre los algoritmos básicos de la aritmética. Además, algunos debates como el que originó este tuit

sobre determinantes, me han convencido de que quizá sea hora de hacer un repaso al tema. Esta entrada es el comienzo de una serie sobre los algoritmos de las matemáticas básicas (entendidas como las matemáticas previas a la universidad). El ritmo será el que se pueda, y durará lo que me dure la cuerda, y/o el interés de los lectores.

Mi intención es seguir el orden en que van apareciendo en el currículo, pero antes de empezar a hablar de sumas y restas creo que merece la pena hacer algunas consideraciones generales.

Me parece que sigue sin estar nada claro cuál es el papel de los algoritmos en estos tiempos, cuando estamos rodeados de dispositivos que hacen todo tipo de cálculos, de forma más rápida y más fiable de lo que lo podrá hacer ningún ser humano. Creo que debería ser uno de los temas centrales de debate en didáctica de las matemáticas, y me parece que no lo está siendo. Por supuesto, lo que voy a exponer aquí son solo mis opiniones, ya me gustaría tener datos. Además, estas opiniones van evolucionando con el tiempo.

Voy a tratar de resumir en un párrafo mis reflexiones sobre el tema, que se pueden ver en versión ampliada en esta presentación, donde recojo mi intervención en la mesa redonda que la IX Escuela Miguel de Guzmán dedicó al tema.

Me parece evidente que el estudio de los algoritmos no puede ser ya un fin en sí mismo, como lo era, de forma justificada, hasta hace unos cuantos años. Mi tesis de inicio es que un algoritmo merecerá ser estudiado si, no solo se entiende, sino que ayuda a comprender ideas y conceptos que sean relevantes. Algunas veces se oye que a algunos alumnos les gusta calcular, por el puro gusto de calcular. Bien, no tengo problema en aceptar eso. Pero todos tenemos nuestros gustos y aficiones, y que haya un colectivo al que le resulte atractiva la actividad X no es razón para imponer esa actividad a toda la población. Sobre todo, si resulta que hay otros alumnos a los que esa imposición/requerimiento les aleja de la disciplina completa, o les impone una dificultad adicional, muchas veces decisiva, en el aprendizaje de las matemáticas.

Un último comentario previo: un mismo algoritmo se puede presentar de muchas formas. En particular, en la figura se muestran dos ejemplos que corresponden al algoritmo tradicional de la suma, y que probablemente corresponden a tratamientos bastante distintos del mismo. Cuando hablemos de un algoritmo, habrá que asumir que se trata de forma adecuada o, en todo caso, discutir en qué consistiría esa presentación adecuada.

Si queremos hablar de algoritmos para sumar y restar en los primeros cursos de primaria,  deberíamos tener claro antes cuáles son los conceptos fundamentales de esa etapa, y que deberían ser desarrollados en paralelo con los algoritmos. Este caso me parece claro: la notación posicional y, más en general, el sentido numérico.

Empezando por la suma, voy a considerar tres algoritmos distintos. Primero, una presentación rápida, y después hablaré de las ventajas e inconvenientes que les veo.

1. El tradicional, mostrado en la figura anterior, y que no necesita presentación.
2. Explorando sobre el tema me encontré con un vídeo de un alumno que sumaba como se muestra en la figura.
   Me parece una propuesta muy interesante, y que también puede verse como otra forma de escribir la suma en fila
   
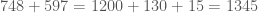
   Me parece evidente que escribir la suma como en la figura facilita los cálculos al alumno.
3. Los algoritmos ABN. Creo que ya son bastante conocidos, pero aquí va una presentación en dos líneas «en aras de la completitud».  El acrónimo proviene de algoritmos Abiertos Basados en Números. En la tabla de la derecha se muestra un ejemplo. Si queremos sumar los números 36 y 43, lo que se hace es disponer lainformación en una tabla, e ir pasando cantidades del número menor al mayor. Evidentemente, cuando hemos pasado el número completo, en la casilla correspondiente aparece la suma final. La forma de pasar es flexible, y alumnos con diferentes habilidades de cálculo encontrarán caminos distintos (de ahí el adjetivo de abiertos). Creo que la escritura no está del todo estandarizada (se puede argumentar que no hace falta, por supuesto) y si se buscan ejemplos es posible que no aparezca la columna de la izquierda del ejemplo, las cantidades que se van pasando. En este blog se puede encontrar más información.

Voy a atreverme a aventurar unas pocas reflexiones sobre comparación de estos algoritmos, dejando claro que son reflexiones personales, que han cambiado en estos últimos años, que pueden cambiar en el futuro próximo, y que tengo más preguntas que respuestas.

En primer lugar, decir que el algoritmo tradicional me parece una buena opción. Eso sí, por supuesto, trabajando con números del tamaño adecuado al desarrollo del alumno, y no «llevándome 1», sino reagrupando las 12 unidades en una decena y dos unidades, con el apoyo gráfico/manipulativo necesario.

El algoritmo 2 me gusta mucho. Creo que usa de forma muy natural la notación posicional, y que cuando se calculan sumas de esta forma se está haciendo un uso intenso de las descomposiciones numéricas. Su gran ventaja, me parece, es que se adapta muy bien a las técnicas de cálculo mental y cálculo aproximado. Si queremos hacernos a la idea del orden de magnitud de una suma, es evidente que debemos a sumar desde la izquierda. Solo le veo un inconveniente, y es que no veo cómo trasladarlo al caso de la resta, como veremos más abajo. Y creo que este es un inconveniente muy serio. La pregunta surge sola: ¿sería adecuado trabajar los algoritmos 1 y 2, en paralelo o de forma secuencial? Creo que solo una posible experiencia de aula nos podría iluminar en este punto.

Sobre el ABN, entiendo el éxito relativo que están teniendo en las aulas. Lo que me parece que ocurre en muchos casos es que sustituyen a un tratamiento puramente mecánico del algoritmo tradicional. Y claro, tras años de ver que tus alumnos no entienden nada, hacer por fin algo que se entiende tiene un atractivo evidente. Sobre el algoritmo en sí mismo, es desde luego un buen ejercicio de cálculo mental. Pero si se piensa (como es mi caso) que una de las razones fundamentales de trabajar un algoritmo de la suma es trabajar la comprensión de la notación posicional, entonces creo que surgen muchas dudas. Por los ejemplos que se ven en la red, y por lo que he visto hacer a mis alumnos al tratarlos en la asignatura de aritmética, no me parece que profundizar en la comprensión de la notación posicional sea su fuerte. Pero esta cuestión está abierta, desde luego.

Para terminar con la suma, por supuesto que otra alternativa sería olvidarse de algoritmos, trabajar el cálculo mental (pensado), desarrollando las estrategias adecuadas, de forma realmente flexible, y pasar a la calculadora cuando el tamaño de los números lo requiera.

La resta.

Restar es intrínsecamente más difícil que sumar. Y esto se evidencia tanto en la comprensión del concepto como en los algoritmos. Empezando por los algoritmos tradicionales, hay dos formas de arreglar el problema que surge cuando la cifra del minuendo es menor que la correspondiente del sustraendo.

En el recuadro rojo de la figura (la resta de la izquierda) se muestra el algoritmo tradicional en España (y en otros países europeos). Aquí el problema de cómo se presenta en las aulas es claro. Decir «me llevo una» en el caso de la suma puede ser poco adecuado, pero en el caso de la resta es simplemente disparatado. No hay una, ni me la llevo a ningún sitio. Estamos simplemente trasladando la cantilena de la suma a una situación completamente distinta. Desde luego, con ese lenguaje es imposible que los alumnos entiendan nada, y mi impresión es que muchos niños empiezan a naufragar con la introducción del algoritmo de la resta. La idea para justificar el algoritmo es sencilla, otra cosa es que sea natural, o fácil de captar por el alumno de 1º-2º de primaria. Lo que hace el algoritmo es usar la propiedad de compensación: sumamos 10 unidades al minuendo y 1 decena al sustraendo. La diferencia se mantiene, y ya podemos hacer la cuenta. El lenguaje que se ha usado en España para presentar este algoritmo deja bien claro que la comprensión nunca ha estado entre nuestras preocupaciones a la hora de enseñar matemáticas.

La alternativa de la derecha, usada en el mundo anglosajón y en Asia (y llegando a nuestras aulas) consiste en desagrupar una decena, expresándola como 10 unidades. En el ejemplo, en lugar de 4 decenas y 2 unidades, tenemos 3 decenas y 12 unidades, y ya podemos seguir con el cálculo. Lo que he visto en las aulas es que se usa el término «prestar» y tampoco me parece adecuado, porque creo que deberíamos enseñar a nuestros alumnos que lo que te prestan tienes que devolverlo, y aquí no hay devolución posible. Creo que la verbalización del procedimiento debe estar adaptada al vocabulario de los niños, por supuesto, pero también debe reflejar el proceso de manera correcta. ¿Tomamos una decena, y la expresamos como 10 unidades? Quizá haya mejores alternativas. De nuevo, la experiencia de aula es imprescindible.

La mayor dificultad de la resta queda en evidencia al tratar de buscar un análogo del segundo algoritmo para la suma. No veo alternativa mejor que la que muestra la figura, basada en una idea que circuló por twitter hace unos días.

Seguramente sea un ejercicio interesante, para 1º de la ESO, para trabajar la aritmética de los enteros, y hacer eso tan importante, y que tan pocas veces hacemos, que es reflexionar sobre las conexiones entre diferentes temas. Pero si hablamos de algoritmo para la resta en 2º-3º de primaria, no me parece una alternativa.

En cuanto a los algoritmos ABN, en la figura se muestra un ejemplo. Me parece que la tabla es suficientemente explícita: voy quitando del número mayor, y cuando lo he quitado todo me encuentro con la diferencia.

Para terminar, una breve comparación. Sobre los ABN, los comentarios son los mismos que para la suma. Y no es casualidad, porque las ideas subyacentes son exactamente las mismas, claro.

De nuevo aquí se puede aplicar el comentario final sobre la suma: una opción podría ser prescindir de los algoritmos en columna (y de las tablas de los ABN), trabajar (con números del tamaño adecuado al desarrollo de los alumnos) técnicas de cálculo pensado, y recurrir a la calculadora cuando los números sean más grandes.

Finalmente, mi opinión sobre las dos alternativas para gestionar «las llevadas»: no conozco ningún resultado basado en trabajo de aula, pero estoy convencido de que hacer reagrupamientos en el minuendo es más natural que usar la compensación aumentando el sustraendo. Y creo que hay cierto consenso en el tema, a juzgar por cómo la primera de las alternativas va ganando terreno en las aulas y en los libros de texto. Otra cosa son los problemas que la transición está causando, con libros que empiezan con una alternativa para luego usar otra más adelante, o colegios donde se hace algo parecido, o el desconcierto de algunas familias cuando se encuentran con que no saben cómo resta su hijo. Este es otro tema, que quizá merezca tratarse en otra entrada, esta ya es demasiado larga.