Es un placer anunciar que el libro de Alexander Zvonkin, Matemáticas de 3 a 7 años, del que hablé hace ya unos años, acaba de ser publicado en la colección Estímulos Matemáticos, una colaboración entre la Real Sociedad Matemática Española y la editorial SM. Más información, aquí.
Archivos de categoría para Primaria
A vueltas con los libros de texto
Como cada comienzo de curso, hemos asistido al cruce de argumentos habitual sobre el tema de los libros de texto, su excesivo coste, el buen o mal uso que se hace en las aulas, hasta he llegado a ver que el libro de texto, como concepto en sí mismo, no porque sea de mala calidad, es en parte responsable del fracaso escolar …
Como llevo un tiempo sin escribir sobre el tema, creo que es hora de volver a tratarlo. Me gustaría centrarme en los aspectos puramente educativos, y para tratar de evitar que un posible debate se desvíe por otros caminos, voy a empezar con una serie de comentarios preventivos.
- Sí, desde hace unos meses estoy involucrado en un proyecto editorial. No, esa no es la causa de que defienda, con los matices que sea, las ventajas de unos buenos libros de texto. La flecha de la causalidad va en dirección contraria: como siempre he pensado que un buen libro de texto es una buena herramienta, tanto para el profesor como para el alumno, cuando ha surgido la ocasión no he dudado en involucrarme en un proyecto que trata de llevar mejores textos de matemáticas a nuestras aulas.
- Muchas de las quejas que se escuchan sobre el excesivo coste de los libros de texto en España pueden estar bastante justificadas. Pero eso puede tener que ver con el excesivo número de asignaturas que hay en todos nuestros niveles educativos (bueno, ahí la universidad es una excepción, creo que reducir el número de asignaturas en los grados fue lo más positivo de la «reforma Bolonia» de hace unos años).
- Desde luego, el coste de los libros de texto no debería ser una barrera para el acceso a la educación de los niños de familias en situaciones económicas difíciles. Y me parece perfectamente defendible que los libros de texto los deberíamos pagar entre todos, vía impuestos, y no las familias. Pero es una decisión política, que se debe tomar en los foros correspondientes.
- Un lugar común es que a las editoriales no les interesa la educación, que «solo quieren ganar dinero». Bueno, eso es bastante cierto, ya lo pensaba y nada de lo que he visto últimamente me ha hecho cambiar de opinión. Pero eso no pasa solo con las editoriales y la educación, sino con casi todo en la sociedad en que vivimos, empezando por ejemplo con temas igual de importantes, como la alimentación o la sanidad. Si estamos tranquilos con respecto a lo que comeremos mañana (al menos, los que tenemos la suerte de disfrutar de una situación económica desahogada) no es porque tengamos alrededor entes solidarios que se preocupen de nuestras necesidades, sino porque confiamos en el afán de lucro del panadero, el supermercado, o el restaurador que ponen a nuestra disposición lo necesario, a cambio, claro, de un pago. El tema de la sanidad tiene todavía más aristas, como el papel de los laboratorios farmacéuticos en algunos de los escándalos que han surgido últimamente, el problema de la distribución de medicamentos en los países menos desarrollados, o la falta de investigación en el desarrollo de nuevos antibióticos, por las pocas perspectivas de rendimiento económico que tiene. Creo que los gobiernos deberían tener un papel mucho más activo en este tema, y corregir muchas de las prácticas que vemos. Lo que no me parece una alternativa es recomendar a los ambulatorios que cultiven sus propias cepas de penicilina. En resumen: no creo que sea ningún problema que las editoriales quieran ganar dinero. Creo que el problema es que en España lo consigan con productos tan mediocres.
- Seguiré usando el término «libro de texto», aunque es evidente que estamos en un proceso de cambio, y que no está nada claro qué tipo de materiales veremos en nuestras aulas dentro de 10 años, creo que falta mucho por aprender sobre las implicaciones cognitivas de distintas opciones, y hay datos como éste, como mínimo, dan que pensar.
Paso ya al debate estrictamente educativo.
- El primer argumento que se suele escuchar es que «un buen profesor no necesita un libro de texto». Eso es cierto, sin duda. Un buen docente (o, mejor, un equipo bien cohesionado) bien formado y trabajador puede hacer un trabajo estupendo sin libros de texto. Lo sé, conozco ejemplos. La pregunta importante es si esa práctica es generalizable a todo el sistema escolar. No es fácil conseguir datos fiables de esto, pero las informaciones que me llegan es que, en los países donde parece que las cosas funcionan razonablemente bien, uno de los factores que ayudan son unos buenos libros de texto. Si algún lector conoce algún país donde parezca que los resultados educativos son buenos, y que ha decidido prescindir de los libros de texto, me encantaría explorar el caso.
- El problema es cuando se le da la vuelta a la afirmación anterior, cometiendo la falacia más común, la de dar la vuelta a una implicación que solo funciona en un sentido, y se afirma, o se transmite, que los profesores que usan libros de texto es porque no son tan buenos, o tan trabajadores, o les falta iniciativa. Y creo que esta visión se ha extendido bastante, en particular en nuestros centros de formación de maestros. La visión mayoritaria es que un buen maestro elabora sus propios materiales, y en lugar de prepararles para elegir buenos textos y usarlos bien se les prepara para que elaboren unidades didácticas. Aquí la universidad está a la cabeza, porque la ANECA, el organismo que rige la carrera profesional de los profesores universitarios (hay que ser evaluado por ella cada vez que queremos progresar), decidió hace años «dar puntos» a los profesores que elaboran sus propios materiales. Puestas así las cosas, cuando el profesor X tiene que impartir el curso próximo una asignatura como Cálculo para Ingenieros, tiene dos opciones:
- recurrir a uno de los 3 ó 4 manuales estándar de la asignatura, que son los usados en las mejores universidades del mundo. Además de que no recibirá ninguno de esos puntos si opta por esto, tendrá que luchar contra lo poco acostumbrados que estarán sus alumnos a usar un libro de texto. La mayoría habrán recurrido a ellos solo para hacer algún trabajo, y para hacer los ejercicios K y L de la página J.
- elaborar sus propios apuntes. En este caso, los alumnos estarán más contentos, y el profesor recibirá esos puntitos de la ANECA. Por supuesto, nadie comprobará si esos apuntes son buenos, malos o regulares. Esta situación me temo que va a peor, porque se está trasladando al procedimiento de evaluación de la docencia que están implementando cada vez más universidades, presionadas por la superioridad en ese sentido.
Aunque cada vez es más complicado saber qué se hace en cada sitio (una consecuencia creo que desafortunada del desarrollo de los entornos de ayuda al aprendizaje virtual), no es difícil imaginar hacia dónde se deslizan las cosas con la actual estructura de incentivos …
- Lo que me resulta más llamativo es que esta situación de una mayoría de estudiantes nada acostumbrados a usar con criterio libros de texto convive con el énfasis que se pone en la importancia del «aprender a aprender». Es verdad que en estos tiempos cualquiera que quiera aprender algo tiene a su disposición materiales estupendos, pero me parece difícil que alguien que está aprendiendo tenga el criterio para elegir algunos de entre los más adecuados. Ya sé que hay experiencias realmente sorprendentes sobre lo que se puede conseguir en esta dirección, lo que no conozco es comparativas con lo que habrían conseguido esos niños con buenos libros de texto y buenos maestros a su alrededor.
- Una imagen que escuché en una presentación de Marshall Cavendish, que no había oído, y que me ha gustado mucho, es esta analogía con la música: el libro de texto es la partitura, y el profesor es el intérprete. Me encanta el jazz, y por supuesto que valoro la música improvisada, pero también soy consciente de lo que aporta un buen intérprete a cualquier partitura, por muy escrita que ya esté. En el aula, un docente no tiene por qué limitarse a seguir mecánicamente el libro de texto, como a veces se critica. Cuando un niño dice «no lo entiendo», o hace una pregunta interesante, o hace algo mal, la reacción del profesor para conducir la situación, localizar la dificultad de aprendizaje, o buscar un enfoque alternativo que solucione el problema, es lo que diferencia al docente excelente del bueno, o del menos bueno.
- En resumen, a la afirmación del principio de «un buen profesor no necesita un libro de texto» (que como dije suscribo) contrapondría esta otra, que también me parece cierta: «un buen libro de texto es una excelente herramienta para cualquier profesor (y para los alumnos)».
Los currículos en espiral
A raíz de este artículo publicado en El Español el pasado domingo, del vídeo donde se habla de la repetición de contenidos en España, y de su mención a cómo estudian las fracciones en Singapur, me han hecho algunas preguntas interesantes, y he pensado que la mejor forma de tratar de contestarlas podría ser rescatar una de las entradas en la cola de borradores, la dedicada al tema de los currículos en espiral.
Nuestros currículos, ya desde la LOGSE, están diseñados en espiral. Pero si nos fijamos en los currículos de Singapur, también dicen que su diseño es en espiral. Lo que sigue es un extracto de la introducción al currículo de matemáticas de primaria de 2007.
Care has been taken to ensure that there is continuity from the primary to the secondary levels. Using a spiral design of the curriculum, each topic is revisited and introduced in increasing depth from one level to the next. This enables students to consolidate the concepts and skills learned and then further develop them.
El 2013 cambiaron el currículo de primaria, y este curso llegan a 4º (van a curso por año, no como aquí …). Siguen mencionando el diseño en espiral, como puede comprobarse en esta página, donde también se puede ver la estructura general de las diferentes etapas educativas. Una aclaración preventiva: no tengo datos de cuántos alumnos cursan esas matemáticas fundamentales de 5º y 6º de primaria, ni estoy defendiendo esa separación tan temprana. Tampoco tengo datos de cómo funcionan esas pasarelas que aparecen en etapas posteriores de la estructura. Esos aspectos organizativos son relevantes, pero no me parece un tema estrictamente curricular. En todo caso, cuando se piense en ello merece la pena tener en la cabeza cuál es la alternativa que usamos en España, y que es la que parece que peor funciona: la repetición de curso.
Volviendo al diseño en espiral, puede ser un poco exagerado decir que en España estudian en todos los cursos lo mismo, pero me parece claro que hay demasiada repetición. Se introducen las fracciones en 3º, y en 4º de primaria ya suman fracciones (lo cual no me parece malo en sí mismo), pero algo falla, porque siguen repitiendo la suma en 5º y en 6º, y como cualquier profesor de primeros cursos de ESO podrá corroborar, sigue siendo necesario trabajarla en 1º y 2º de secundaria, y sigue siendo fuente de errores durante toda la etapa. Algo parecido pasa con la multiplicación y la división (empezando en este caso en 5º). Esto no es solo un problema de los alumnos con más problemas de aprendizaje. Ya sé que es solo una anécdota, pero me parece significativa: el otro día una compañera de departamento que imparte la asignatura de Probabilidad y Procesos Estocásticos en 2º de Ingeniería de Telecomunicación, me contaba que en un problema aparecía la suma de una serie, y que el obstáculo para una cantidad significativa de sus alumnos había sido darse cuenta de que . El problema me parece claro: en ningún momento se le dedica a cada cosa el tiempo suficiente para poder lograr un auténtico aprendizaje comprensivo, que es el único que permite que ese conocimiento siga allí cuando los alumnos vuelven de las vacaciones de verano.
En Singapur, por el contrario, no repiten los conceptos. Introducen el concepto de fracción, y comparan, suman y restan fracciones con el mismo denominador en 2º, en 3º tratan los mismos temas pero con el caso de denominadores distintos (eso sí, manteniendo los números del tamaño adecuado para que el alumno entienda lo que está haciendo), en 4º las fracciones impropias, la fracción de un conjunto, y los números mixtos (esto último me parece que sobra, se podría decir eso de «nadie es perfecto»), en 5º tienen dos temas, tratan la multiplicación y la división de una fracción entre un entero, y por último en 6º aparecen fracciones como divisores, y hacen un pequeño repaso. Por si algún lector quiere algún detalle más, aquí he reunido los índices de los temas de fracciones de los textos de Marshall Cavendish. No es el currículo oficial, pero el lector que compare estos índices con el currículo enlazado anteriormente comprobará que la precisión del currículo deja poco margen para los contenidos (no voy a entrar aquí en si esto es bueno o malo, seguramente es posible en un país pequeño, uniforme y centralizado como Singapur, mucho más complicado en España, pero ese es otro tema). Por supuesto en los conceptos y procedimientos tratados en cursos anteriores aparecen en actividades y problemas de cursos posteriores, pero creo que eso es completamente distinto a estudiarlos de nuevo. En cuanto a secundaria, en 1º aparecen cuatro páginas de repaso, eso es todo.
Un último documento: los índices de los libros de primaria. Creo que son suficientes si algún lector quiere hacerse una idea de cómo tratan otros temas.
Y un comentario final: decir que un currículo está diseñado en espiral no es decir gran cosa. El diablo está en los detalles, y un calificativo como ése se puede aplicar a realidades muy diferentes.
¿Campaña por un nuevo currículo de matemáticas?
Este año también me fui de vacaciones con la intención de volver con ideas para promover algún tipo de acción pidiendo una revisión de los currículos de matemáticas. Y supongo que, como en años anteriores, la intención se habría quedado en eso, sepultada por el resto de tareas que uno se encuentra de cara al comienzo de curso, de no haber sido por este tuit de hace unos días:
La imagen del tuit es la transparencia 54 del powerpoint de este informe, que me parece interesante en general.
Creo que la gran mayoría de los profesores estamos de acuerdo en que los currículos son demasiado extensos. De hecho, este problema ha empeorado con la LOMCE. Si los informes de organizaciones a las que se recurre tan a menudo cuando se habla de competencia matemática coinciden en que es mejor elegir menos contenidos, para poder tratarlos en profundidad, ¿no debería este tema llegar al debate social? Seguramente las asociaciones de profesores podrían ser la opción natural, pero mis (escasos) intentos en el pasado reciente han tenido resultado cero. Creo que ha llegado el momento de intentar sacar partido de las nuevas tecnologías, y ensayar la participación directa. El objetivo de esta entrada es (aparte de tratar de forzarme a dar el paso) pedir opinión a los lectores, y recabar ideas. ¿Conocéis alguna alternativa que pudiera ser más adecuada que Change.org?
Fin de curso … IX Escuela Miguel de Guzmán
Lo que me parecía imposible hace un año ha resultado no serlo tanto: este fin de curso ha sido todavía más ajetreado que el anterior. No es una queja, porque la mayoría de las tareas son estrictamente voluntarias, y estoy muy contento de cómo van. Algún viaje profesional, las evaluaciones de mis alumnos, el trabajo con los libros de Singapur que llegan a los coles el próximo septiembre y, como guinda, el trabajo en la organización de la IX Escuela Miguel de Guzmán. El objetivo de esta entrada es pasar a limpio mis conclusiones sobre estas jornadas, y que además esto sirva como cierre del curso.
Lo primero, tal y como me comprometí durante la Escuela, aquí están enlazados los materiales que varios de los ponentes y encargados de los talleres ponen a disposición de la comunidad. ¡Gracias!
Para empezar por el final, la sensación que me quedó al terminar la Escuela fue, como otras veces en estos casos, agridulce. Para ser justos, dulce, pero con un pequeño toque agrio. Por supuesto, fueron días llenos de debates interesantes, intercambio de ideas y propuestas, y muy formativos. El toque agrio viene de la sensación de que estábamos reunidos una parte de la comunidad docente que estamos de acuerdo en muchas cosas, pero quizá olvidando que sigue habiendo una mayoría a la que no llegan estos mensajes. Es verdad que hubo algunas intervenciones en los debates de participantes que manifestaron que participaban en este tipo de eventos por primera vez, que le habían interesado mucho, y que volvían a casa con muchas cosas sobre las que pensar. En resumen: objetivo cumplido, y un detalle en el que creo que podríamos mejorar, tratar de llegar a una parte mayor de la profesión.
Lo que quiero hacer en el resto de esta entrada es dejar por escrito algunos comentarios sobre las ponencias, incluyendo también alguna observación crítica, cuando toque.
Clara Grima, en la conferencia inaugural, nos demostró que se pueden decir cosas muy interesantes, y ser divertida, a la vez. No es algo que se vea con excesiva frecuencia en nuestro mundo …
Cecilia Calvo nos habló de las tareas ricas: su observación fundamental es que hay habilidades básicas que hay que practicar, pero que muchas veces esa práctica se puede hacer a través de esas tareas ricas, donde además hay involucradas actividades con valor cognitivo. En su presentación hay varios ejemplos, y en el espacio Puntmat muchos más. Me parece una propuesta muy interesante, con una sola debilidad: creo que para llevar esto al aula se necesitan docentes muy bien formados.
Juan Francisco Hernández, del Hispano-Inglés de Santa Cruz de Tenerife, nos habló de la clase invertida. Creo que merece la pena echar un vistazo a los materiales que ha puesto a nuestra disposición. No voy a entrar en el debate de fondo sobre la clase invertida, pero sí quiero mencionar que cuando se piensa en una metodología habría que tener en cuenta que una cosa es funcionar bien, o muy bien, con un docente – o un equipo docente – determinado (formado, trabajador, etc), y en un centro determinado, y otra cosa es que esa metodología sea generalizable al sistema escolar. Recomiendo estas reflexiones de El Lolaberinto sobre el tema.
Irene Ferrando habló sobre modelización. En su presentación (15 Mb) hay varios ejemplos muy interesantes. Por otra parte, aquí se aplica la misma observación del párrafo anterior, sobre metodologías «exportables», y un comentario adicional: en un vídeo donde nos enseñaba un proyecto de estimación de la cantidad de papel de aluminio en un colegio (el proyecto me pareció muy interesante) vimos a un alumno con la famosa «escalera de las unidades», subiendo peldaños y añadiendo ceros (¿o quitándolos?, nunca lo recuerdo). Los proyectos, la modelización, o la clase invertida, pueden ser buenas herramientas para motivar a nuestros alumnos (y esto es un valor en sí mismo, lo sé), pero creo que si no cambiamos algunas cosas de fondo, los resultados sobre el aprendizaje real serán limitados.
Para terminar, Lurdes Figueiral, la presidenta de la asociación de profesores de matemáticas de Portugal, nos presentó el currículo producto de la reforma de 2011. No recuerdo haber oído nada al respecto (sí, me temo que soy uno más de esa mayoría social que hace bien poco caso a lo que ocurre en nuestro vecino del oeste), pero parece que fue una reforma curricular bastante polémica, hecha en contra de la profesión. La impresión que trasladó Lurdes Figueiral fue muy negativa. Aquí está el currículo. El aspecto no es bueno, desde luego. Un interminable listado de contenidos … Una cosa, al menos, me gusta: los autores dan la cara, en primera página. La reforma se hizo bajo el mandato de un ministro de educación con formación de economista-matemático, Nuno Crato.
No asistí a ningún taller, fueron los ratos que dediqué a las gestiones organizativas, pero todos los comentarios que escuché fueron positivos.
En cuanto a las mesas redondas, al final las dos giraron en torno al tema de en qué debería consistir el aprendizaje matemático elemental (para mí, entendido como el correspondiente a la educación obligatoria) en estos tiempos. En la mesa de las calculadoras, Juan Emilio García nos mostró un par de vídeos que provocaron los momentos más hilarantes de la Escuela. Parece ser que los vídeos ya estaban en youtube. Yo no los conocía, y los quiero compartir aquí, porque además de divertidos me parece que tienen su interés didáctico.
El primero es una muestra perfecta de por qué hay que dedicarle algo de atención a enseñar a usar las calculadoras:
En el segundo, tres de las estrellas del humor español de los 70, con los cambios de unidades, y nuestra querida regla de tres …
Para terminar, como le dediqué cierto tiempo a pensar sobre mi intervención en la mesa redonda «Las matemáticas en la educación obligatoria del Siglo XXI», pensé que sería buena idea guardar esas reflexiones de alguna forma. En lugar de escribirlas, lo que he hecho es preparar un vídeo, porque me ha servido además de primera práctica con la herramienta ActivePresenter. Su versión gratuita me ha parecido bastante potente, y sencilla de empezar a usar.
Sirva este vídeo (20 min) de despedida por este curso. ¡Feliz verano a todos los lectores!
¿Memorizar las tablas?
Otra entrada breve para responder a una pregunta surgida de este tuit (sigo con la idea de cerrar el curso con mis impresiones de la Escuela Miguel de Guzmán).
Es un tema muy interesante, sobre el que seguramente vuelva en el futuro, pero creo que puedo dar una primera respuesta rápida.
Creo que el punto clave es aclarar los dos posibles significados del término «memorizar» en el aprendizaje matemático. Uno puede estar hablando de «aprender de memoria» las tablas de multiplicar, como si fuera la lista de los reyes Godos, o los afluentes del Duero por la derecha. Esto es lo que pide el currículo LOMCE de Madrid donde, sin mencionar nada que tenga que ver con la idea de multiplicación, y en ¡1º de Primaria!, aparece un punto que dice «Memorizar las tablas del 0, el 1, el 2 y el 5». Hay muchas barbaridades en el currículo de primaria de la LOMCE, pero creo que si tuviera que dar un primer premio esta sería mi elección.
Pero creo que también se puede usar el término memorizar refiriéndose al estado final de aprendizaje. Se puede trabajar la multiplicación, y uno de los resultados finales del proceso debería ser que el alumno sepa de memoria las tablas de multiplicar. No sé lo suficiente de psicología del aprendizaje (mejor dicho, no sé nada) para profundizar en las diferencias cognitivas, pero como matemático me parece claro que son enfoques distintos y que son el resultado de procesos de aprendizaje diferentes.
En el tema de las tablas de la suma es evidente que Aharoni está hablando de esta segunda forma de memorizar, porque se detiene a tratar el tema de cómo sumar dos números de una cifra, y del problema de pasar «la frontera del 10», en el ejercicio de calcular la suma 8+5. Esta es una etapa crucial del aprendizaje de la suma. Los niños que aprenden/descubren técnicas de cálculo flexible, de descomposición numérica, y que piensan en 5=2+3 para concluir que 8+5 = 10 + 3 = 13, son niños que van en la buena dirección en el camino del aprendizaje de las matemáticas. Por el contrario, los niños que hacen esta cuenta basada en memorizar (en el primer sentido) las tablas de la suma, o simplemente contando, están avanzando en una dirección con peores resultados de aprendizaje.
En el tema de la multiplicación la cosa queda menos clara, me parece que por el problema del significado del signo «x» en la multiplicación, del «veces» o «multiplicado por» del que ya hemos hablado aquí. Me resulta muy significativo que un buen matemático (en el sentido de investigador en matemáticas) con amplia experiencia en aulas de primaria, se mueva en este tema de forma insegura. Está claro que es un tema que no tenemos resuelto. Mi impresión es que si adoptamos el término «veces», el significado de la multiplicación queda mucho más claro, y el aprendizaje de las tablas de multiplicar puede estar basado en la comprensión. Sobre este tema espero poder dar algo más de información durante el próximo curso. En los libros de 2º de Primaria de Polygon ya aparecen las tablas (el 2, el 3, el 4, el 5 y el 10), y estarán presentes en algunas de nuestras aulas este próximo curso.
Por último, sobre el libro de Aharoni. Lo tenía un poco aparcado, pero este tema me ha hecho revisarlo, y coincido con @danicapoblog en que sería muy positivo tener el libro accesible en castellano, como ayuda para esas familias, me parece que cada día más numerosas, que son conscientes de los problemas en el aprendizaje matemático de sus hijos, pero que no terminan de entender cuál es el problema de fondo, o que no tienen las herramientas para luchar contra él. Me apunto el tema para septiembre.
Shanghai-Singapur
Tenía pensado cerrar el curso con una entrada sobre la Escuela Miguel de Guzmán, pero este tweet se ha cruzado en mis planes.
Lo único que había visto hasta ahora de Shanghai era sus excelentes resultados en las pruebas de siempre. No parece que sea sencillo conseguir información. No he encontrado su currículo en inglés, y los textos que usan allí tampoco están en inglés. Parece que este tema ha surgido por el proyecto de implantar estas metodologías en colegios (de primaria) de Gran Bretaña. Aquí hay algo de información sobre Shanghai, y algunos materiales de muestra (de los primeros cursos de primaria).
En este otro enlace de Maths no Problem se puede leer una comparativa sobre Singapur y Shanghai. Creo que debo avisar de que es una comparativa interesada: Maths no Problem es la editorial británica que empezó a trabajar con Marshall Cavendish, la editorial más importante de Singapur. Recientemente Marshall Cavendish se ha aliado con Oxford University Press (aquí) y creo que Maths no Problem está trabajando con otra editorial de Singapur. En cualquier caso (y aunque mi opinión también puede estar sesgada, desde luego), creo que tienen bastante razón en lo que dicen. La fortaleza esencial de Shanghai puede ser la excelente preparación de su profesorado, mientras que la metodología de Singapur puede depender menos de la excelencia del docente (eso no quiere decir que lo ideal no sea tener buenos docentes, claro, en este espacio no creo que haya que hablar de una función de varias variables).
Lo que sí es cierto sobre Singapur, y esto lo he repetido muchas veces en las últimas semanas, presentando los libros de Polygon Education en los colegios de la zona de Madrid, es que la metodología de Singapur se hizo famosa, a nivel internacional, por su éxito en el movimiento homeschooling de EEUU. ¿La razón? Creo que sencilla: los padres descubrieron que «esas matemáticas» sí las entendían. Y también es cierto que en Singapur eligieron la metodología teniendo bien presente que sus docentes de hace 30 años tenían una formación más bien tirando a básica. Las cosas han cambiado, desde luego (por ejemplo, los profes de Singapur tienen 100 horas de formación continua obligatoria al año. Vamos, 6 veces más que aquí en cantidad. Y apuesto a que en calidad también nos aventajan) pero creo que algo de esa idea de «facilidad de presentación» todavía subsiste.
Termino con una especulación: el lector atento se puede haber dado cuenta de que detrás de los materiales de Shanghai que enlacé arriba está Collins, otra de las grandes editoriales británicas. Es posible que la razón de que aparezca Shanghai sea simplemente que es la forma que Collins ha encontrado de unirse al movimiento de renovación en Gran Bretaña, porque allí el gobierno ha puesto mucho dinero en este tema.
Una nota sobre formación matemática de maestros
Este artículo de El Diario, de @hcebolla, habla sobre calidad de profesores, y creo que su lectura merece la pena. Pero lo que me ha dejado impactado es este gráfico:
Los datos corresponden al estudio TEDS-M sobre formación matemática de maestros (en concreto, de estudiantes de último año de la antigua diplomatura de magisterio de primaria). Los datos de la izquierda son los resultados de los diferentes centros de formación de maestros españoles que participaron (casi todos los pertenecientes a universidades públicas, y algunos de universidades privadas). Los datos de la derecha corresponden a los centros de EEUU. Como en casi todo estudio, la variabilidad en los resultados de los centros estadounidenses es llamativa, pero también me resulta de lo más llamativa la uniformidad (en la mediocridad) de los resultados de los centros españoles.
No conozco otro estudio con esta uniformidad. En PISA 2012, por ejemplo, los resultados por comunidades autónomas variaron entre los 517 puntos de Navarra y los 461 puntos de Extremadura. En TEDS-M, donde la unidad de estudio es de menor tamaño, lo esperable sería que la variabilidad fuera mayor.
Llevo unos días dándole vueltas al tema, y sigo tan perdido como al principio, de forma que en lugar de aventurar una explicación prefiero abrir la puerta a un posible debate.
La prueba externa de 6º en Cataluña
Ayer vi la prueba externa de 6º de primaria que han hecho en Cataluña. En mi opinión, bajo ese manto de «Competencias matemáticas» y «situaciones reales» lo que hay es una prueba que, desde el punto de vista de los conceptos matemáticos involucrados, es muy, muy sencilla. Quizá tenga sentido evaluar este tipo de competencias, pero yo diría que tiene más que ver con la comprensión lectora que con los conocimientos matemáticos de final de primaria. Seguramente dentro de unas semanas algún político saldrá diciendo que los resultados han sido buenos, pero nos estaremos haciendo trampas al solitario.
La prueba está en catalán, pero creo que se entiende muy bien. En cualquier caso, voy a hacer el ejercicio de traducir las preguntas, prescindiendo de «adornos» y «situaciones». Por supuesto, esto pone las cosas más fáciles, pero el trabajo que hay que hacer para pasar de los enunciados originales a estos otros es (sólo un poco de) comprensión lectora.
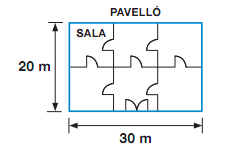
El pabellón de la figura está formado por 6 salas iguales.
- En una sala caben 60 personas. Si las 6 salas están llenas, ¿cuántas personas hay?
a) 350 b) 360 c) 500 d) 600 - ¿Cuánto mide el perímetro del pabellón?
a) 50 m b) 60 m c) 100 m d) 120 m - En la feria se hacen 30 actividades. La mitad (1/2) son por la mañana, y 2/4 partes por la tarde. Señala la afirmación correcta:
a) Hay más actividades por la mañana
b) Hay más actividades por la tarde
c) Hay el mismo número de actividades por la mañana y por la tarde.
Justifica tu respuesta. - En la feria hay un campeonato de robots con 4 pruebas de 15 minutos cada una. Si las pruebas son seguidas y deben terminar a las 17:30 horas, ¿a qué hora debe empezar la primera prueba?
a) A las 16:00 b) A las 16:15 c) A las 16:30 d) A las 16:45 - El colegio tiene 90 entradas. ¿Cuántas entradas hay que repartir a 6º si le corresponden el 10 % del total?
a) 9 b) 18 c) 20 d) 80
- Se prepara una mesa de 6 m de largo como la de la figura.
Se coloca 1 silla cada metro, y un robot cada 2 metros.
¿Cuántas sillas y cuántos robots hay que colocar?
a) 3 sillas y 2 robots b) 5 sillas y 3 robots
c) 6 sillas y 2 robots d) 6 sillas y 3 robots - Tenemos mesas
 cuadradas de 1 m x 1 m, y cuando juntamos dos o tres mesas las personas se sientan como indica la figura.Hay que juntar 4 mesas, y tenemos las dos posibilidades de la figura. ¿En cuál de ellas se podrán sentar más personas? (Justifica tu respuesta)
cuadradas de 1 m x 1 m, y cuando juntamos dos o tres mesas las personas se sientan como indica la figura.Hay que juntar 4 mesas, y tenemos las dos posibilidades de la figura. ¿En cuál de ellas se podrán sentar más personas? (Justifica tu respuesta)
Unos robots transportan pirámides como la de la figura. - ¿Cuántos vértices tiene la pirámide?

a) 3 b) 4 c) 5 d) 6 - ¿Cuántas aristas tiene la pirámide?
a) 5 b) 6 c) 7 d) 8Queremos hacer un cubo con piezas como esta (se muestra un cubito unidad).
Hasta ahora hemos hecho lo que se muestra en la figura.
- ¿Cuántas piezas como ésta (se muestra un cubito unidad) tiene la figura?
a) 9 b) 12 c) 15 d) 18 - ¿Cuántas piezas faltan para completar el cubo?
a) 6 b) 9 c) 12 d) 18Los robots se clasifican en 4 categorías:
- ¿A qué categoría pertenece un robot que pesa 3/4 de kilo?
a) 1 b) 2 c) 3 d) 4 - ¿Cuánto pesan 3 robots de la categoría 2?
a) Menos de 2 kg b) Entre 2 kg y 3 kg c) Más de 3 kg y menos de 4 kg d) Más de 4 kgObserva la figura. Las dos ruedas pesan lo mismo que las 10 piezas.
- Si cada rueda pesa 100 gr, ¿cuánto pesa una pieza?
a) 10 gr b) 20 gr c) 200 gr d) 400 gr - Los robots A y B siguen un recorrido. El robot A se para cuando ha recorrido 1/4 de un circuito de 120 cm. ¿Cuántos centímetros ha recorrido?
a) 30 cm b) 60 cm c) 90 cm d) 480 cm - Cada 2 segundos un robot recorre 20 cm. ¿Cuántos centímetros habrá recorrido al cabo de 6 segundos? (La figura de ayuda está incluida en el enunciado)
a) 40 cm
b) 60 cm
c) 80 cm
d) 100 cm - El robot A cambia de dirección como se indica en la figura.

¿Cuántos grados gira a la derecha?
a) Gira 15º
b) Gira 45º
c) Gira 60º
d) Gira 90º - Los robots A y B recorren el mismo circuito. El robot A tarda 50 segundos y el robot B tarda 1 minuto y 15 segundos. Señala la afirmación correcta:
a) El robot A tarda 15 segundos más que el robot B.
b) El robot A tarda 25 segundos más que el robot B.
c) El robot B tarda 15 segundos más que el robot A.
b) El robot B tarda 25 segundos más que el robot A.
 En la tabla de la figura se muestran el número de alumnos de 5º y 6º que han participado en las distintas categorías. (Cada alumno participa en una sola categoría.
En la tabla de la figura se muestran el número de alumnos de 5º y 6º que han participado en las distintas categorías. (Cada alumno participa en una sola categoría. - ¿Cuántos alumnos han participado en la categoría de robots rastreadores?
a) 17 b) 18 c) 25 d) 35 - ¿Cuántos alumnos de 5º (cinqué) han participado en las tres categorías? (Aquí creo que el enunciado no es del todo claro)
a) 17 b) 18 c) 38 d) 39
- Según la tabla, en las tres categorías han participado
a) más alumnos de 5º que de 6º
b) los mismos alumnos de 5º que de 6º
c) más alumnos de 6º que de 5º
d) 18 alumnos de 5º y 17 alumnos de 6º - En la categoría de rastreadores habría más participantes de 6º que de 5º si en 6º hubiera participado
a) 1 alumno más b) 2 alumnos más c) 3 alumnos más d) 4 alumnos más
 En la figura se muestra un código de movimientos.
En la figura se muestra un código de movimientos.
Creo que se entiende. - Para ir del punto 3 al punto 4 de la figura, ¿cuál es la secuencia correcta?

- Un robot se encuentra en el punto 5 de la figura y sigue estas instrucciones.
 Dibuja la figura y escribe alguna de sus características.
Dibuja la figura y escribe alguna de sus características. - Martín tiene 4 bolsas y cada bolsa contiene 5 paquetes de vasos con 25 vasos en cada paquete. ¿Qué operación permite calcular el número total de vasos?
a) 4 + 5 + 25 b) 4 + 5 x 25 c) 4 x 5 + 25 d) 4 x 5 x 25 - Una bebida cuesta 1,45 euros. ¿Cuál es el precio aproximado de 6 bebidas?
a) 6 b) 8 c) 9 d) 12 - El desayuno de un grupo cuesta 18,75 euros y el desayuno de otro grupo, menos numeroso, cuesta 10,15 euros. ¿Cuál es el precio más aproximado del desayuno de los dos grupos juntos?
a) 27 b) 28 c) 29 d) 30Observa esta relación: el precio de un bocadillo y una botella de agua es el mismo que el de 3 zumos.
- Si un bocadillo cuesta 1,80 euros y una botella de agua cuesta 1,20 euros, ¿cuál es el precio de un zumo?
a) 1 b) 2 c) 3 d) 4 - Para desayunar también hay fruta. En una caja de 60 piezas de fruta hay 30 manzanas. ¿Qué fracción del total de frutas son manzanas?
a) 1/2 b) 1/3 c) 1/4 d) 1/6Con piezas como las de la izquierda se hace una figura como la de la derecha.

- ¿Cuántas piezas hay de tipo A?
a) 2 b) 4 c) 8 d) 10 - ¿Cuántas piezas hay de tipo B?
a) 4 b) 8 c) 10 d) 12
Me parece que la prueba se parece más a ésta de California (3º de Primaria) que a ésta, también de California, o a ésta, de Alberta (Canadá), ambas de 6º de Primaria. No me refiero, claro está, a los conocimientos de pre-álgebra, que no son contenidos de nuestra primaria, sino a la parte de aritmética, geometría y tratamiento de la información. Me parece que las preguntas que hacen tienen mucho más contenido matemático que las de esta prueba externa de Cataluña.
Si hablamos de pruebas internacionales, el nivel de esta prueba no me parece más avanzado que el que reflejan estas preguntas liberadas del estudio TIMSS de 4º de Primaria. Si esto es lo que vamos a entender por evaluar la «competencia matemática» me parece que no vamos por buen camino …
Escuela Miguel de Guzmán
Hoy una entrada breve para anunciar la IX Escuela de Educación Matemática Miguel de Guzmán, organizada de forma conjunta por la Federación Española de Sociedades de Profesores de Matemáticas y la Real Sociedad Matemática Española.
Será los días 6-7-8 de julio, en la Universidad de Alcalá. El título de la Escuela es «Qué enseñar y cómo hacerlo: nuevas metodologías», y aunque me gustaría que el programa tuviera más espacio para discutir el «qué», antes de pasar al «cómo», algo hay en esa dirección, y espero que la participación del profesorado ayude. El plazo de inscripción es del 2 de mayo al 20 de junio.
Más información en la página de la FESPM y en la de la RSME.
Y éste es el cartel anunciador, por si tenéis ocasión de ponerlo en vuestros centros.