Ayer vi la prueba externa de 6º de primaria que han hecho en Cataluña. En mi opinión, bajo ese manto de «Competencias matemáticas» y «situaciones reales» lo que hay es una prueba que, desde el punto de vista de los conceptos matemáticos involucrados, es muy, muy sencilla. Quizá tenga sentido evaluar este tipo de competencias, pero yo diría que tiene más que ver con la comprensión lectora que con los conocimientos matemáticos de final de primaria. Seguramente dentro de unas semanas algún político saldrá diciendo que los resultados han sido buenos, pero nos estaremos haciendo trampas al solitario.
La prueba está en catalán, pero creo que se entiende muy bien. En cualquier caso, voy a hacer el ejercicio de traducir las preguntas, prescindiendo de «adornos» y «situaciones». Por supuesto, esto pone las cosas más fáciles, pero el trabajo que hay que hacer para pasar de los enunciados originales a estos otros es (sólo un poco de) comprensión lectora.
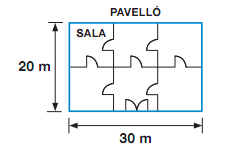
El pabellón de la figura está formado por 6 salas iguales.
- En una sala caben 60 personas. Si las 6 salas están llenas, ¿cuántas personas hay?
a) 350 b) 360 c) 500 d) 600 - ¿Cuánto mide el perímetro del pabellón?
a) 50 m b) 60 m c) 100 m d) 120 m - En la feria se hacen 30 actividades. La mitad (1/2) son por la mañana, y 2/4 partes por la tarde. Señala la afirmación correcta:
a) Hay más actividades por la mañana
b) Hay más actividades por la tarde
c) Hay el mismo número de actividades por la mañana y por la tarde.
Justifica tu respuesta. - En la feria hay un campeonato de robots con 4 pruebas de 15 minutos cada una. Si las pruebas son seguidas y deben terminar a las 17:30 horas, ¿a qué hora debe empezar la primera prueba?
a) A las 16:00 b) A las 16:15 c) A las 16:30 d) A las 16:45 - El colegio tiene 90 entradas. ¿Cuántas entradas hay que repartir a 6º si le corresponden el 10 % del total?
a) 9 b) 18 c) 20 d) 80
- Se prepara una mesa de 6 m de largo como la de la figura.
Se coloca 1 silla cada metro, y un robot cada 2 metros.
¿Cuántas sillas y cuántos robots hay que colocar?
a) 3 sillas y 2 robots b) 5 sillas y 3 robots
c) 6 sillas y 2 robots d) 6 sillas y 3 robots - Tenemos mesas
 cuadradas de 1 m x 1 m, y cuando juntamos dos o tres mesas las personas se sientan como indica la figura.Hay que juntar 4 mesas, y tenemos las dos posibilidades de la figura. ¿En cuál de ellas se podrán sentar más personas? (Justifica tu respuesta)
cuadradas de 1 m x 1 m, y cuando juntamos dos o tres mesas las personas se sientan como indica la figura.Hay que juntar 4 mesas, y tenemos las dos posibilidades de la figura. ¿En cuál de ellas se podrán sentar más personas? (Justifica tu respuesta)
Unos robots transportan pirámides como la de la figura. - ¿Cuántos vértices tiene la pirámide?

a) 3 b) 4 c) 5 d) 6 - ¿Cuántas aristas tiene la pirámide?
a) 5 b) 6 c) 7 d) 8Queremos hacer un cubo con piezas como esta (se muestra un cubito unidad).
Hasta ahora hemos hecho lo que se muestra en la figura.
- ¿Cuántas piezas como ésta (se muestra un cubito unidad) tiene la figura?
a) 9 b) 12 c) 15 d) 18 - ¿Cuántas piezas faltan para completar el cubo?
a) 6 b) 9 c) 12 d) 18Los robots se clasifican en 4 categorías:
- ¿A qué categoría pertenece un robot que pesa 3/4 de kilo?
a) 1 b) 2 c) 3 d) 4 - ¿Cuánto pesan 3 robots de la categoría 2?
a) Menos de 2 kg b) Entre 2 kg y 3 kg c) Más de 3 kg y menos de 4 kg d) Más de 4 kgObserva la figura. Las dos ruedas pesan lo mismo que las 10 piezas.
- Si cada rueda pesa 100 gr, ¿cuánto pesa una pieza?
a) 10 gr b) 20 gr c) 200 gr d) 400 gr - Los robots A y B siguen un recorrido. El robot A se para cuando ha recorrido 1/4 de un circuito de 120 cm. ¿Cuántos centímetros ha recorrido?
a) 30 cm b) 60 cm c) 90 cm d) 480 cm - Cada 2 segundos un robot recorre 20 cm. ¿Cuántos centímetros habrá recorrido al cabo de 6 segundos? (La figura de ayuda está incluida en el enunciado)
a) 40 cm
b) 60 cm
c) 80 cm
d) 100 cm - El robot A cambia de dirección como se indica en la figura.

¿Cuántos grados gira a la derecha?
a) Gira 15º
b) Gira 45º
c) Gira 60º
d) Gira 90º - Los robots A y B recorren el mismo circuito. El robot A tarda 50 segundos y el robot B tarda 1 minuto y 15 segundos. Señala la afirmación correcta:
a) El robot A tarda 15 segundos más que el robot B.
b) El robot A tarda 25 segundos más que el robot B.
c) El robot B tarda 15 segundos más que el robot A.
b) El robot B tarda 25 segundos más que el robot A.
 En la tabla de la figura se muestran el número de alumnos de 5º y 6º que han participado en las distintas categorías. (Cada alumno participa en una sola categoría.
En la tabla de la figura se muestran el número de alumnos de 5º y 6º que han participado en las distintas categorías. (Cada alumno participa en una sola categoría. - ¿Cuántos alumnos han participado en la categoría de robots rastreadores?
a) 17 b) 18 c) 25 d) 35 - ¿Cuántos alumnos de 5º (cinqué) han participado en las tres categorías? (Aquí creo que el enunciado no es del todo claro)
a) 17 b) 18 c) 38 d) 39
- Según la tabla, en las tres categorías han participado
a) más alumnos de 5º que de 6º
b) los mismos alumnos de 5º que de 6º
c) más alumnos de 6º que de 5º
d) 18 alumnos de 5º y 17 alumnos de 6º - En la categoría de rastreadores habría más participantes de 6º que de 5º si en 6º hubiera participado
a) 1 alumno más b) 2 alumnos más c) 3 alumnos más d) 4 alumnos más
 En la figura se muestra un código de movimientos.
En la figura se muestra un código de movimientos.
Creo que se entiende. - Para ir del punto 3 al punto 4 de la figura, ¿cuál es la secuencia correcta?

- Un robot se encuentra en el punto 5 de la figura y sigue estas instrucciones.
 Dibuja la figura y escribe alguna de sus características.
Dibuja la figura y escribe alguna de sus características. - Martín tiene 4 bolsas y cada bolsa contiene 5 paquetes de vasos con 25 vasos en cada paquete. ¿Qué operación permite calcular el número total de vasos?
a) 4 + 5 + 25 b) 4 + 5 x 25 c) 4 x 5 + 25 d) 4 x 5 x 25 - Una bebida cuesta 1,45 euros. ¿Cuál es el precio aproximado de 6 bebidas?
a) 6 b) 8 c) 9 d) 12 - El desayuno de un grupo cuesta 18,75 euros y el desayuno de otro grupo, menos numeroso, cuesta 10,15 euros. ¿Cuál es el precio más aproximado del desayuno de los dos grupos juntos?
a) 27 b) 28 c) 29 d) 30Observa esta relación: el precio de un bocadillo y una botella de agua es el mismo que el de 3 zumos.
- Si un bocadillo cuesta 1,80 euros y una botella de agua cuesta 1,20 euros, ¿cuál es el precio de un zumo?
a) 1 b) 2 c) 3 d) 4 - Para desayunar también hay fruta. En una caja de 60 piezas de fruta hay 30 manzanas. ¿Qué fracción del total de frutas son manzanas?
a) 1/2 b) 1/3 c) 1/4 d) 1/6Con piezas como las de la izquierda se hace una figura como la de la derecha.

- ¿Cuántas piezas hay de tipo A?
a) 2 b) 4 c) 8 d) 10 - ¿Cuántas piezas hay de tipo B?
a) 4 b) 8 c) 10 d) 12
Me parece que la prueba se parece más a ésta de California (3º de Primaria) que a ésta, también de California, o a ésta, de Alberta (Canadá), ambas de 6º de Primaria. No me refiero, claro está, a los conocimientos de pre-álgebra, que no son contenidos de nuestra primaria, sino a la parte de aritmética, geometría y tratamiento de la información. Me parece que las preguntas que hacen tienen mucho más contenido matemático que las de esta prueba externa de Cataluña.
Si hablamos de pruebas internacionales, el nivel de esta prueba no me parece más avanzado que el que reflejan estas preguntas liberadas del estudio TIMSS de 4º de Primaria. Si esto es lo que vamos a entender por evaluar la «competencia matemática» me parece que no vamos por buen camino …