El máximo común divisor

El pasado sábado hubo una interesante conversación en twitter alrededor del máximo común divisor y los algoritmos para calcularlo. @druizaguilera proponía este diagrama conjuntista para determinar los factores comunes: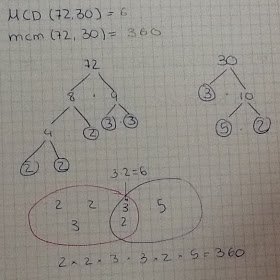

@raulf aportó este otro enfoque:

todo empezó con este tuit del pasado 7 de febrero: https://twitter.com/dacilgonz/status/696336412078186498

Estos días he seguido dándole vueltas al tema, y han cristalizado algunas ideas sobre las que llevaba tiempo pensando.

El primer comentario es que los métodos propuestos son realmente algoritmos para calcular intersecciones de multiconjuntos, y mi gran pega es que enseñan muy poco sobre qué es el máximo común divisor. Mi impresión es que la mayor dificultad de este tema no es el cálculo, sino la comprensión del concepto, para poder aplicarlo en la resolución de problemas. Del vídeo que enlacé en su día sobre lo que hacían mal en Singapur en los años 70, me interesa cada vez más una de las cosas que se mencionan: los procedimientos y la comprensión conceptual hay que trabajarlos en paralelo (el vídeo dura 5 min, y este tema se empieza a tratar a los 40 seg):

Para trabajar en paralelo la comprensión y el cálculo del mcd (y del mcm) me parece más interesantes las actividades que proponen Cecilia Calvo y David Barba en su trabajo publicado en SUMA, y que los autores han puesto aquí (vía @druizaguilera).

El tema del máximo común divisor y el mínimo común múltiplo lo trato en magisterio, a todos los alumnos les suena la receta de «factores comunes …», y lo hacen bien, en general, sin necesidad de procedimientos ad hoc. Lo que me sorprende es que ninguno parece estar familiarizado con el hecho de que a partir de la factorización de un entero es fácil escribir el conjunto de sus divisores, lo cual es tanto como decir que no tienen idea de por qué funciona la receta que usan para calcular el máximo común divisor. Creo que es un tema sencillo de entender, no hay más que pararse a comparar el conjunto de divisores de un número como 36 con su factorización. La relación entre factorización y divisores da mucho juego (estos temas han sido para mí un descubrimiento reciente, a raíz de impartir clases en magisterio: la aritmética elemental está llena de relaciones que dan lugar a auténtico pensamiento matemático). Por ejemplo, a partir de la relación entre factorización y divisores se pueden contar el número de divisores de un entero: si $n = p^2\cdot q^3\cdot r$ (p, q y r son números primos distintos, claro), entonces n tiene 24 divisores. A la inversa (examinar un problema al revés es una de las mejores formas de profundizar en su comprensión), puedo construir números con, por ejemplo, 18 divisores, de estas formas: $p^8\cdot q$ , $p^5\cdot q^2$, $p^2\cdot q^2 \cdot r$ . ¿Cuál es el número más pequeño que tiene 18 divisores?

Hay otro aspecto quizá incluso más importante. Los pedagogos dicen (y en este punto estoy de acuerdo con ellos) que algo se ha aprendido de verdad cuando el conocimiento se puede transferir a otra situación. Y aquí radica la extraordinaria potencia del método matemático: que las ideas y las estrategias que involucra son transferibles a una cantidad sencillamente sorprendente de situaciones. Cuanto más especializado sea un procedimiento, menos transferible será. No dudo de que las propuestas del principio de esta entrada sean útiles para que los alumnos hagan los cálculos necesarios para superar el examen correspondiente, lo que dudo es qué quedará de todo eso un año después de haber hecho ese examen.

Suena familiar, ¿verdad?

Una minientrada, para recomendar encarecidamente la visión de este vídeo (5 minutos). En él se habla de lo que hacían mal en Singapur enseñando matemáticas hace 40 años. ¿No resulta inquietantemente familiar?

(Quiero dar las gracias a David Ayerra, del colegio Irabia-Izaga, de Pamplona, que no sólo me ha dado a conocer el vídeo sino que lo ha subtitulado).

Técnicas versus conceptos

La conferencia de clausura de la jornada sobre innovación que mencioné en la entrada anterior fue impartida por Michèle Artigue. No la conocía (soy un recién llegado al campo de la educación matemática) pero se trata sin duda de una primera figura a nivel internacional. Recientemente ha recibido nada menos que el premio Felix Klein en el año 2013 y la medalla Luis Santaló en el año 2014, dos de las distinciones mas importantes en el área.

La primera parte de su conferencia la dedicó a presentar unos materiales sobre los que estaban trabajando. Me parecieron interesantes. La idea era modelar con Geogebra problemas de persecución. Ahora no encuentro una referencia, pero cuando la consiga volveré a hablar sobre este tema.

Después su conferencia se deslizó hacia aspectos mas abstractos de la didáctica. Antes de seguir, una aclaración preventiva: no pretendo cuestionar el interés de esta didáctica mas abstracta. Lo único que digo es que demasiadas veces peca de excesivamente académica, y alejada de la realidad de las aulas y que, por tanto, puede no resultar del todo accesible e interesante para el profesor de a pie. Este problema no es, desde luego, exclusivo de la didáctica. De hecho, creo que los matemáticos caemos en este error con bastante frecuencia. Para dar un ejemplo en el que he caído personalmente, empeñarse en hablar de epsilones y deltas – o del Teorema de Bolzano – a futuros ingenieros. Y también ocurre en otras áreas alejadas de las matemáticas. La mas prominente me parece el bombardeo de análisis sintáctico y morfológico en los estudios de Lengua de nuestra secundaria.

Total: que en esos aspectos abstractos de la didáctica me perdí completamente, y estuve distraído unos minutos hasta que escuché una expresión ya oída, la teoría antropológica de lo didáctico. Ya me había topado con la etiqueta en alguno texto, sin llegar a entender casi nada, así que intenté concentrarme de nuevo en la conferencia, para ver si conseguía sacar alguna idea en claro. Nuevo fracaso: la jerga me resulta incomprensible. Si algún lector sabe algo del tema, y puede expicar en qué consiste en lenguaje accesible a profanos, le estaré sinceramente agradecido.

De manera que nuevos minutos de distracción, hasta que escuché una frase, pronunciada con total convicción. que captó de nuevo mi atención. Creo que, textualmente (habla un castellano bastante correcto), Artigue dijo: «Pensar que, gracias a las TIC, podemos prescindir de las técnicas y centrarnos en el estudio de los conceptos es un profundo error». Es una frase que suscribo completamente, pero se trata solo de la entrada al problema, claro. Es una pena que no hubiera tiempo para profundizar en el tema (era ya el final de la conferencia, no hubo turno de preguntas, y la reunión terminaba justo entonces) porque me parece una de las grandes cuestiones de la educación matemática en nuestros días.

Desde mi punto de vista, la clave es que existe una fuerte relación entre algunas técnicas y los conceptos. Dicho de otra forma: para comprender de forma adecuada ciertos conceptos es importante adquirir cierta soltura técnica. Ahora bien, creo que es crucial entrar en el detalle. Por poner un ejemplo sencillo: estoy de acuerdo en que hacer divisiones es importante para comprender los problemas de reparto y, en general, para adquirir sentido numérico. Ahora bien, si el valor fundamental del cálculo de divisiones es éste, es muy posible que tengamos que revisar cómo hacer las divisiones, y qué divisiones hacer. Por una razón muy sencilla: el algoritmo tradicional de la división se diseñó con un objetivo muy distinto, que no es otro que poder hacer divisiones exactas con enteros grandes. Si este objetivo ha quedado obsoleto (personalmente, creo que sí), es muy posible que el algoritmo tradicional haya quedado también obsoleto. Revisar los currículos con esta idea en la cabeza puede ser una tarea apasionante. Si hubiera que hacer un concurso sobre el algoritmo mas caduco, por superfluo a la hora de ayudar a la comprensión conceptual, mi voto creo que sería para la Regla de Ruffini. ¿Y el suyo?

La derivada en 1º de Bachillerato (II)

Parece que está claro que el tema de cómo tratar la derivada en 1º de Bachillerato genera cierto debate. Me parece muy bien, siempre ha sido uno de los objetivos de este blog. Sigue en la lista una entrada sobre cómo se trata la introducción de la derivada en otros lugares, pero antes de eso me ha parecido conveniente aclarar los datos sobre uno de los argumentos más repetidos (no sólo en los comentarios, también siempre que hablo del tema con amigos profes). Se oye con bastante insistencia eso de que las derivadas se complican enseguida porque «es lo que les van a pedir en selectividad». Como digo, es una tarea que tenía pendiente, y este debate me ha decidido a vencer la pereza y lanzarme a ello. Estos son los ejercicios que involucran una derivada en las PAU de Madrid en los últimos cuatro años, aquellos a los que tengo fácil acceso en mi universidad.

Junio de 2010:
Opción A, ej. 4. Preguntan los intervalos de crecimiento y decrecimiento de la función $f(x) = \ln(x^2+4x-5)$ .
Septiembre de 2010:
Opción B, ej. 2. Preguntan representación e intervalos de concavidad de la función $f(x) = \displaystyle \frac{3x^2+5x-20}{x+5}$ .
Junio de 2011:
Opción A, ej. 3. Extremos absolutos de la función $f(x)=\sqrt{12-3x^2}$ .
Opción B, ej. 1. Para qué valor de a la función $\displaystyle f(x)=\frac{ax^4+1}{x^3}$ tiene un mínimo relativo en x=1. Para ese valor, encontrar los extremos absolutos.
Septiembre de 2011:
Opción A, ej. 1. Hallar el conjunto de puntos en los quela función $f(x)=\sqrt{x^2-9x+14}$ tiene derivada.
Junio de 2012:
Opción A, ej. 3. Dada $f(x)=x^3+ax^2+bx +c$ , hallar a, b y c para que f alcance en x=1 un mínimo relativo y tenga en x=3 un punto de inflexión.
Opción B, ej. 1. Dada $\displaystyle g(x)=(\ln x)^x$, calcula g'(e).
Septiembre de 2012:
Opción A, ej. 1. Dada la función definida a trozos $f(x)=3x+A$ si $x\leq 3$ y $f(x)=-4+10x-x^2$ si $x>3$ , halla los puntos en que la derivada se anula y los extremos absolutos en el intervalo [4,8].
Opción B, ej. 2. Calcula la ecuación de la recta normal a la gráfica de $f(x)=x^2 \sin x$ (en un punto dado).
Junio de 2013:
Opción A, ej. 3. Ecuación de la recta tangente en un punto a la gráfica de $\displaystyle f(x)=\frac{x^3}{(x-3)^2}$ .
Opción B, ej. 1. Extremos absolutos y puntos de inflexión de $f(x)=2\cos^2 x$ en el intervalo $[-\pi/2,\pi/2]$ .
Septiembre de 2013:
Opción A, ej. 1. Intervalos de crecimiento y decrecimiento de la función $\displaystyle f(x) = \frac{4}{x-4}+\frac{27}{2x+2}$ .
Opción B, ej. 3. Ecuación de la recta tangente en un punto a la gráfica de $\displaystyle f(x) = \frac{x}{x^2+1}$ .

Mi conclusión es clara: la mayoría de los ejercicios de cálculo de derivadas que he visto en el cuaderno de mi hija tras dos semanas de derivadas en 1º de Bachillerato son más complicados que los que aparecen en la PAU. Insisto: ya sé que la intención es la mejor, y por supuesto no tengo claro cómo de generalizado está este enfoque, pero todo me hace pensar que no vamos por buen camino. Y, por supuesto, tampoco estoy diciendo que este problema sea específico del bachillerato. En la Universidad, en muchos aspectos, caemos en el mismo tipo de errores.

La derivada en 1º de Bachillerato

Hoy una minientrada, con un anuncio y un comentario para intentar iniciar un debate.

El anuncio es el de la Escuela de Educación Matemática Miguel de Guzmán. La organizan de forma conjunta la Federación Española de Sociedades de Profesores de Matemáticas y la Real Sociedad Matemática Española. Será en Madrid, del 9 al 11 de julio. La inscripción es gratuita y se cierra el 30 de junio. El objetivo es que sea un punto de encuentro para todos los niveles educativos, y personalmente estaría encantado de que consiguiéramos que asistieran maestros de primaria interesados en las matemáticas.

Y sobre las derivadas, un breve comentario con el ánimo de iniciar un debate: mi hija estudia 1º de Bachillerato, y empezaron el estudio de las derivadas hace dos semanas. Hoy me encuentro en su cuaderno cosas como estas: $\displaystyle y = \ln \sqrt {\frac{1+\cos x}{1-\cos x}}$ o $y = x^{\ln (x+1)}$ . Y hasta parece que ha tenido suerte, porque preguntándole a una amiga del otro grupo me dice: «nuestro profesor nos ha avisado de que los ejercicios del libro son demasiado fáciles».

Como siempre que comento un tema así: nada más lejos de mi intención que criticar a los profesores, sé que lo hacen con la mejor intencion, para que «aprendan más». Pero estamos errando el tiro completamente. No sé cómo de generalizado está este enfoque, pero me temo que concuerda bastante con lo que luego vemos en las aulas del primer curso universitario: demasiados alumnos que no entienden absolutamente nada … Como digo, mi idea hoy es sólo tratar de animar el debate. Estoy preparando una entrada hablando del estudio de las derivadas que he visto en un libro para preparar el A-level (la prueba preuniversitaria de Singapur y otros países anglosajones).

Las reglas de divisibilidad

Ahí siguen en el nuevo currículo de primaria ya publicado en el BOE: «Conoce y aplica los criterios de divisibilidad por 2, 3, 5, 9 y 10». Resulta curiosa la elección de los posibles divisores, porque si al final de primaria hay que hablar de un «criterio de divisibilidad por 2», o por 10, es que la cosa va muy mal … Por otra parte, ¿por qué 9 si, y 4 y 8 no? Pero no quiero entrar hoy en discusiones curriculares, sino que me gustaría centrarme en las matemáticas.

Lo primero que habría que aclarar es que, más que reglas de divisibilidad, de lo que habría que hablar es de cálculo de restos (naturalmente, sin necesidad de hacer la división). Y me parece un matiz importante: cuando empiezo a tratar el tema con mis alumnos de magisterio, todos tienen claro cuándo un número es divisible por 5. Sin embargo, si escribo en la pizarra 5427 y les pregunto que cuál es el resto al dividir entre 5, pocos tienen claro que la respuesta es inmediata, y que no hace ninguna falta calcular el cociente. En el caso del divisor 5 (y, naturalmente, para el 2 y el 10) es realmente muy sencillo, y no veo ninguna razón para que los alumnos no lo tengan totalmente claro al terminar primaria. De hecho, creo que trabajarlo junto con la división es una buena forma de profundizar en la comprensión de la división con resto.

Durante mis dos primeros cursos en la Facultad de Educación, traté este tema con la maquinaria de las congruencias. La primera razón para hacerlo fue que el cálculo de congruencias me parece una oportunidad excelente para «pensar desde cero». El tema no es difícil, pero eso de que 2+1 = 0 (módulo 3), es algo que pone a prueba la capacidad de abstracción de los alumnos. Sigo pensando lo mismo pero, teniendo en cuenta el escaso tiempo disponible, y las dificultades que seguimos detectando en contenidos más básicos, pensamos que lo mejor era dejar el cálculo de congruencias fuera del programa. Lo que hemos hecho estos últimos cursos es tratar el tema con el punto de vista de «aritmética con restos», que resulta más rápido y mucho más cercano a los contenidos de primaria.

Volviendo a las «reglas de divisibilidad», la siguiente, en orden de dificultad, es la del 4. Entender que para calcular el resto al dividir por 4 es suficiente considerar las unidades y las decenas es una aplicación básica de las descomposiciones de números, y de que 100 es múltiplo de 4. La observación es la de siempre: no tiene ningún sentido dedicarle horas y horas a ejercicios de descomposiciones numéricas, a lo largo de toda la primaria, cuando la mejor forma de entenderlas de verdad es verlas en acción. Una vez vista la del 4, no cuesta ningún trabajo incluir la del 8.

Y llegamos a las del 3 y el 9. Veamos cómo se puede calcular el resto de 85 al dividir por 3. Como 85 = 80 + 5, el reparto de 85 caramelos entre 3 niños se puede organizar, en etapas, de la siguiente forma: repartimos grupos de 10, y de cada grupo nos sobra, de momento, 1 caramelo. Por tanto, tras esta primera etapa tenemos pendientes de repartir 8 + 5 caramelos. Con este sencillo argumento, ya sabemos que el resto de 85 al dividir por 3 es el mismo que el resto de 8 + 5 al dividir por 3. Una vez entendida la propiedad para números de dos cifras, me parece sencillo ver cómo se extiende al caso general. Lo único que hace falta es darse cuenta de que todas las potencias de 10 tienen resto 1 al dividir por 3. Naturalemente, el caso del 9 es exactamente igual, precisamente porque las potencias de 10 también tienen resto 1 al dividir por 9.

¿Tiene sentido llevar este planteamiento a un aula de primaria? Creo que sí, pero me falta la experiencia de aula para estar más convencido. De lo que sí estoy convencido es de que, si se piensa que no se pueden – o que no hay tiempo para – explicar cómo funcionan ciertas reglas de divisibilidad, lo que habría que hacer es eliminarlas completamente del programa. ¿Qué se perdería? Cuando, a la hora de factorizar un número, se necesite comprobar si es divisible por 3, siempre existe la opción de hacer la división. El problema de introducir la regla sin explicación es el de siempre: hacemos un poco más profundo ese pozo de las matemáticas como conjunto inextricable de rutinas y recetas varias.

Un último comentario: una vez más se dejan fuera del currículo los casos más interesantes. Comprobar que la condición para que un número sea múltiplo de 6 es que lo sea de 2 y de 3 contribuye a mejorar la comprensión de los conceptos de múltiplo y de mínimo común múltiplo. El cálculo del resto me parece una oportunidad perfecta para una actividad de trabajo de aula. Se puede proponer calcular diversos restos al dividir por 2, por 3 y por 6, y buscar patrones en los resultados. Una vez detectado el patrón, entenderlo en términos de «reparto de caramelos» podría estar al alcance de muchos alumnos.

Measurement, de Paul Lockhart

Se trata de un libro realmente excepcional. Ya había mencionado a Paul Lockhart en este blog, en concreto su lamento; en él expone su visión negativa sobre cómo estamos presentando las matemáticas básicas a los chicos. En Measurement Lockhart nos presenta el lado positivo, su visión de cómo se podrían presentar muchos de los conceptos más profundos de la geometría y del análisis. Su propuesta es original y realmente brillante.

No es fácil que un libro de matemáticas sea a la vez interesante para el iniciado y accesible para el profano, pero creo que este libro lo consigue. Desde luego, personalmente he encontrado montones de ideas interesantes, y creo que un lector con formación matemática básica también podría entender la mayoría de los contenidos del libro. Eso sí, Lockhart es honesto desde el principio y abre el libro avisando de que la belleza de las matemáticas requiere esfuerzo y reflexión. Como él dice, la única forma de aprender matemáticas es haciendo matemáticas, y en el texto intercala cuestiones y problemas que deja para el lector (no, no es un libro que incorpore las soluciones de los problemas).

Creo que el secreto del libro es saber elegir el enfoque más accesible para cada idea. La primera parte arranca del problema de medir para presentar muchos de los conceptos más importantes de la geometría clásica. Es difícil elegir un tema: uno de los muchos que me ha gustado es el tratamiento que hace de las cónicas, y quiero mostrar un ejemplo de parte del tratamiento que hace de las elipses.

Hay tres formas de introducir la elipse: (1) una circunferencia deformada; (2) una sección cónica; (3) la definición métrica.

Que la (1) y la (2) son equivalentes es sencillo de ver, a condición de presentar la elipse como la sección de un cilindro, en lugar de la tradicional del cono. Puede parecer un detalle sin importancia, pero creo que en estos pequeños detalles está muchas veces la clave del éxito: elegir con cuidado el mejor argumento, y no tener miedo de salirse de los caminos usuales. Si consideramos la curva intersección de un cilindro con un plano, su proyección ortogonal es una circunferencia. La figura muestra cómo en una proyección ortogonal las medidas en la dirección paralela a la recta de intersección de los planos no cambian, pero en la ortogonal sí.

Pero lo mejor viene ahora: también es fácil ver, sin una sola cuenta, que el conjunto de puntos cuya suma de distancias a dos puntos fijos (los focos) es constante, es el mismo objeto geométrico. El resultado es de Dandelin, de 1822. La idea se muestra en la figura. Si colocamos dos esferas (con el mismo radio que el cilindro) y tocando el plano de la elipse, los puntos de tangencia resultan ser los focos.

Para comprobarlo, fijémenos en la distancia entre un punto P de la curva y f1. Las tangentes desde un punto a una esfera forman un cono, y la distancia entre el vértice de ese cono y el punto de tangencia en la esfera es la misma para todas las tangentes. Por tanto, la distancia entre P y f1 es la misma que la distancia entre P y la circunferencia donde la esfera es tangente al cilindro. Pero esto quiere decir que la suma de las distancias de un punto de la curva a los focos no es más que la distancia entre las dos circunferencias donde las esferas son tangentes al cilindro. Precioso, ¿no?

La primera parte del libro está repleta de contenidos tan interesantes como éste, y por sí misma ya merece la pena, pero es la segunda parte la que me ha resultado más sorprendente, e interesante. A partir del problema del movimiento y de la velocidad, Lockhart introduce el cálculo diferencial, y después el integral. Y lo hace de una forma original y muy bien conseguida. Mi formación en estas áreas fue con el formalismo de Newton, ampliamente mayoritario prácticamente desde los orígenes del tema, y los diferenciales de Leibniz no eran más que un truco para aplicar ciertas reglas mnemotécnicas de forma más sencilla. Lockhart usa los diferenciales de Leibniz a lo largo de todo el tema, y me deja con la duda de si el cálculo diferencial e integral no resulta mucho más fácil de entender de esta forma, al menos para funciones «razonables», que son las que la mayoría de los científicos e ingenieros se van a encontrar en sus disciplinas.

En resumen, un libro absolutamente recomendable.

¿Quién mató a la geometría?

Ayer @lolamenting lanzó una pregunta muy interesante: ¿por qué la geometría está prácticamente desaparecida de nuestras aulas de primaria y secundaria? Contesté en cuanto la leí, casi sin pensar (es difícil sustraerse del todo al lado oscuro de las nuevas tecnologías), diciendo que me parecía una pregunta muy importante, y muy difícil de contestar. Me reafirmo en la primera parte, pero no en la segunda. Desde luego, voy a dar una respuesta especulativa, pero me parece que bastante convincente. Lo que me parece claro es que en la enseñanza de las matemáticas se han producido dos fenómenos muy claros:

A. Los currículos, pero sobre todo la práctica diaria en la mayoría de nuestras aulas, se han deslizado hacia la parte más mecánica de las matemáticas: algoritmos, fórmulas, rutinas, y recetas varias. La resolución de problemas, el razonamiento lógico y la comprensión conceptual son especies en peligro de extinción.
B. La geometría ha perdido peso en el curriculo, pero todavía más en las aulas. Es una de esas partes por las que se suele pasar más deprisa (junto con la estadística).

Mi tesis es bien sencilla: A explica – y es la causa de – B. ¿Qué caracteriza a la geometría? Sin duda, lo importante que son en ella el razonamiento lógico y la resolución de problemas (la comprensión conceptual es simplemente requisito previo de ambos). Esto ya me parece suficiente explicación: tenemos dos fenómenos, A y B,y el primero explicaría el segundo. Si la navaja de Ockham sigue afilada, lo más probable es que sea su causa.

Pero es que además hay varios argumentos adicionales que refuerzan esta explicación: ¿qué geometría se estudia y cómo se hace? Al principio, una buena parte del tiempo se dedica al cálculo de áreas y volúmenes, donde todo se reduce a memorizar una lista de fórmulas mucho mayor de lo necesaria, y a aplicarlas a ejercicios completamente rutinarios. Cuando avanza la secundaria, el estudio de la geometría se inclina claramente hacia el álgebra: en trigonometría, por ejemplo, se dedica mucho más tiempo a las identidades trigonométricas, o a resolver ecuaciones, que a los problemas.

Que esta tendencia está llegando a extremos inquietantes me ha quedado claro con el comentario de @lolamenting en esta entrada: parece que no es extraño encontrar profesores que impiden a los chicos apoyarse en la intuición geométrica para resolver problemas de fracciones. Sin exagerar, me parece que es una de las cosas más alarmantes, e incomprensibles, que he oído en los últimos años.

Por supuesto, en otras partes la situación no es la misma. Termino la entrada con unos ejemplos de los libros de primaria de Singapur. En general, la geometría tiene una presencia mucho mayor que aquí, ya desde primaria. En particular, usan los problemas de ángulos para iniciar a los niños en el razonamiento geométrico, y creo que lo hacen muy bien. Este es un ejemplo de 4º de Primaria:

Este otro de 5º:

y, por último, el de 6º:

Por supuesto, siguen con el tema en secundaria. En algún momento habrá una entrada dedicada a profundizar en este tema.

La división: una operación con dos significados

Quede claro desde el principio: soy consciente de que el tema del que quiero hablar hoy es bien conocido en didáctica. Algún día intentaré escribir sobre por qué las ideas más relevantes de la didáctica llegan tan poco a las aulas.

El problema con la división es que casi toda la energía se dedica al algoritmo, y se deja en segundo lugar su significado. Y me pongo el primero en la lista de pecadores: ya he escrito varias entradas sobre el algoritmo de la división, y esta es la primera sobre su significado. Consideremos estos dos problemas:

Miguel lleva 30 caramelos al colegio, y los quiere repartir por igual entre sus 5 amigos. ¿Cuántos caramelos debe darle a cada uno?
Miguel lleva 30 caramelos al colegio y los reparte por igual entre sus amigos. Si le da a cada amigo 5 caramelos, ¿cuántos amigos tiene?

Si nos planteamos esa pregunta tan extendida (y tan poco conveniente) de si el problema es de sumar, o de restar o de … la respuesta para ambos es la misma: son «problemas de dividir». Sin embargo, el significado de la división es diferente en cada caso. Creo que la forma más sencilla de darse cuenta es pensar en cómo resolvería la situación Miguel si se le planteara a los 5 años, sin ningún conocimiento de los algoritmos tradicionales de la aritmética. Lo que haría en el primer caso, seguramente, sería ir dando caramelos a sus amigos, de uno en uno y por turnos, hasta que se acabaran. Sin embargo, en el segundo caso haría grupos de 5 caramelos, hasta averiguar que le salen 6 de tales grupos.

El primer sentido de la división se conoce como división partitiva, y tiene el sentido de reparto; el segundo es la división cuotativa, y responde a la pregunta de cuántas veces cabe el divisor en el dividendo. Si hacemos el esfuerzo de ponernos en el lugar del alumno que empieza a estudiar la división, llegaremos a la conclusión de que no es tan sencillo concluir que los dos significados se traducen en el mismo algoritmo. Y el problema es que la división cuotativa se trabaja muy poco. El sentido partitivo es, claramente, el más intuitivo, y el mejor para introducir la división, y así se hace siempre. Pero habría que trabajar también el sentido cuotativo de la división, y esto se hace mucho menos. El problema se hace evidente cuando llegan las fracciones y aparece la diferencia más llamativa entre los dos significados de la división: en la división partitiva el divisor es, necesariamente, un número entero; sin embargo, en la división cuotativa, el divisor puede no ser entero. Los alumnos (quizá una mayoría) luchan por dar sentido a eso de «dividir por 1/2» porque se están enfrentando al problema de falta de comprensión adecuada del sentido cuotativo de la división.

Mi impresión es que este detalle no es suficientemente conocido entre los docentes. Y de nuevo me pongo el primero en la lista. Leí sobre el tema preparando mis clases de magisterio del curso pasado, después de llevar un par de cursos bastante perplejo ante las dificultades de una parte significativa de mis alumnos al tratar problemas como «Un grupo de amigos compra 6 pizzas y se las reparten por igual. Si cada amigo come 2/3 de pizza, ¿cuántos amigos son en el grupo?»

Por supuesto, se trata de uno de esos problemas que,una vez detectado, tiene fácil solución. Ya desde el principio, al proponer problemas (antes de presentar el algoritmo), habría que trabajar ambos sentidos de la división.

Una vez más, un problema que se hace evidente en secundaria pero cuyo origen está en la enseñanza primaria.

La inflación terminológica

Como ya me ha ocurrido otras veces, un hecho puntual me decide a escribir sobre un tema al que de alguna manera le estaba dando vueltas. Hojeando un libro de 4º de la ESO me llamó la atención una nueva ecuación de la recta: la ecuación segmentaria. Tuvo una componente casi emocionante: después de casi 30 años dedicado a las matemáticas, todavía podía descubrir una nueva ecuación para una recta en el plano! En el cuadro resumen del mismo libro (el de la foto), comprobé que en ese tema trataban nada menos que ¡7! ecuaciones distintas.

Hablando ya en serio, creo que el problema es más relevante de lo que se puede pensar a primera vista. Es cierto, todas son «equivalentes» (pero, un momento, si son equivalentes, ¿para qué queremos tantas?), y para el profesor, o un alumno que entiende el tema, no suponen ningún problema. Pero creo que para el alumno medio que se enfrenta al tema por primera vez, simplemente memorizar el listado completo de ecuaciones (o el subconjunto que se trate en el curso) y cómo pasar de unas a otras, consume una parte importante de tiempo que luego … no tenemos para hacer problemas. Creo que es sólo un ejemplo de un problema general, que consiste en la sobreabundancia de términos, ecuaciones, clasificaciones, etc. y que, por supuesto, tiene que ver con lo que ya escribí en la entrada sobre la función secante.

Desde luego, el problema no es nuevo. Ya en 1984, Miguel de Guzmán escribía sobre los problemas de la enseñanza de las matemáticas en España, y subrayaba el “énfasis excesivo y perjudicial en nombres y distinciones” [1]. Pero creo que, lejos de corregirse, este problema ha empeorado (en el sentido de que el recorte que se ha producido en los programas – y sobre todo en la práctica – se ha centrado en los problemas, y otras actividades de alto valor cognitivo, y por tanto la proporción problemas/técnicas-definiciones-terminología ha disminuido con el paso de los años).

¿Qué ecuaciones de la recta se deberían tratar en secundaria? Desde mi punto de vista, como mucho los tipos de ecuaciones que aparecen para estudiar curvas y superficies en general, que son las esencialmente distintas:

la paramétrica (si se escribe en forma escalar o vectorial es un detalle que no creo que se merezca un nombre).
la implícita, ax + by + c =0 (llamarle ecuación general, o no, creo que es secundario).
la explícita, y = ax + b, importante por la conexión con las gráficas de funciones y la idea de pendiente.

¿Qué se hace en otros sitios? Bueno, los libros que tengo a mano son los de Singapur. He comprobado los textos de secundaria, comparables a los españoles de la ESO porque allí también tienen 6 años de primaria (empezando a los 6 años) y 4 de secundaria. En tercer curso, en 20 páginas del libro, estudian la recta solo con la ecuación explícita. Por supuesto, le dedican el tiempo necesario al concepto de pendiente, y a las rectas verticales y horizontales, que tantos dolores de cabeza causan a algunos de nuestros alumnos. Después, en 4º curso, le dedican 4 páginas de repaso al tema. Como la ecuación implícita (o general) ya ha aparecido en el estudio de los sistemas lineales, es el momento de hacer algunos ejercicios que aclaren su relación con la explícita, ya conocida del curso anterior. Ya sé que es un solo tema, y un solo país, pero, ¿no resulta la diferencia muy llamativa?

[1] Miguel de Guzmán: El papel de la matemática en el proceso educativo inicial. Enseñanza de las ciencias, 1984, pp. 91-95.

Más ideas, menos cuentas. Un blog sobre educación matemática.

Archivos de etiquetas para Conceptos