Archivos mensuales de marzo 2016

El sorteo de la Champions (y II)

Muchas gracias a todos por las aportaciones. Creo que ha habido tres soluciones distintas, y que tiene sentido recapitularlas.

  1. Con probabilidad elemental, fijando un primer equipo español, digamos el A. La probabilidad de que su rival sea español es 2/7. Que el rival de A no sea español tiene probabilidad 5/7, y en ese caso que el rival de B sea el tercer equipo español tiene probabilidad 1/5. Por tanto, la probabilidad de eliminatoria española era \frac{2}{7} + \frac{5}{7} \cdot \frac{1}{5} = \frac{3}{7}.
  2. Directamente con la regla de Laplace, contando casos favorables y posibles. En algún momento hablaremos de la combinatoria, casi desaparecida del currículo. Y cuando se trata, reducida a variaciones, permutaciones y combinaciones, con sus correspondientes fórmulas. A la hora de la verdad, muchas cosas no son nada de eso. Por ejemplo, los posibles emparejamientos entre n equipos.
    Para la primera eliminatoria hay \binom{n}{2} posibilidades, para la segunda \binom{n-2}{2}, etc. Como es mejor ignorar el orden de esos emparejamientos, tras dividir por (\frac{n}{2})! se obtiene la fórmula para el número de emparejamientos entre n equipos: \frac{\binom{n}{2} \binom{n-2}{2} \cdots \binom{2}{2}}{(\frac{n}{2})!}. Tras simplificar queda (como observó ricardito) que el número de emparejamientos entre n equipos es el producto de los impares menores que n. En el caso de los 8 equipos, 7 \times 5 \times 3.
    ¿En cuántos de ellos hay eliminatoria española? Hay 3 posibles emparejamientos entre equipos españoles, y para cada uno de ellos hay que emparejar los restantes 6 equipos. Por tanto, hay 3 \times 5 \times 3 emparejamientos con eliminatoria española.
  3. Para terminar, mi modelo de las bolas rojas. Consideramos 8 posiciones, distribuidas en 4 cajas. La posición 1 y 2 en la primera caja, la 3 y la 4 en la segunda, etc. Hay \binom{8}{3}=56 formas de colocar 3 bolas en esas 8 posiciones.  Si en una caja hay dos bolas, hay 6 huecos para la bola roja restante. Por tanto, en 4\times 6 de las distribuciones de bolas hay 2 en la misma caja, y la probabilidad es \frac{24}{56} = \frac{3}{7}.

El sorteo de la Champions y los modelos matemáticos

Actualización 3: un lector pregunta por los detalles del sorteo. Creo que lo razonable es aclarar eso al principio. Se trata de un sorteo puro, cualquier combinación es igualmente probable. Los detalles de cómo se lleva a cabo el sorteo «real» son irrelevantes, eso es parte del tema de «elegir bien el modelo», sobre el que quería escribir en esta entrada. En todo caso, simplemente hay 8 bolas en un bombo, y se van extrayendo una a una. Se empareja 1ª con 2ª, 3ª con 4ª, etc.

Tal y como ha quedado la entrada, creo que también es justo avisar a los lectores de que el reto es encontrar el fallo en los dos primeros argumentos. 

———————————————————

A cuenta del sorteo de la Champions, en el que de un total de 8 equipos tenemos 3 españoles, @edusadeci lanzó la pregunta de qué probabilidad hay de que el sorteo empareje a dos equipos españoles, ya advirtiendo de que no es un problema tan sencillo como parece. Merece la pena echar un vistazo a las respuestas, realmente variadas …

Creo que es un ejemplo más de lo difícil que es la probabilidad, y de que muy pronto aparecen preguntas «sencillas» nada fáciles de contestar.

El aspecto que más me interesa del problema es que es un ejemplo perfecto de la importancia de elegir un buen modelo. Desde luego, la probabilidad se puede calcular directamente contando resultados del sorteo. Pero no es sencillo, y es otro buen ejemplo de lo sutil que es la combinatoria, sobre todo dado lo desentrenados que estamos en ella (su presencia en la educación matemática obligatoria es menos que testimonial).

El modelo que me parece más sencillo para contestar la pregunta original es considerar 4 cestos, y 3 bolas rojas. Si colocamos al azar las 3 bolas en los cestos, ¿cuál es la probabilidad de que caigan en cestos distintos? La clave para darse cuenta de que es el mismo problema es considerar las 8 bolas del sorteo, y ver el sorteo como el procedimiento de extraer bolas, al azar, e irlas colocando de dos en dos en los cestos. Podemos imaginar las bolas de los equipos españoles coloreadas de rojo, y darnos cuenta de que realmente el resto de las bolas ¡no juegan ningún papel! Visto así, queda también claro que se trata de una variante del problema del cumpleaños, donde tenemos 3 personas, que cumplen años en 4 días (con probabilidad uniforme, e independientes, claro) y nos preguntamos por la probabilidad de que sus cumpleaños sean distintos.

Una vez hemos llegado aquí, el resto es probabilidad «sencilla». Si numeramos las 3 bolas según el orden en que las colocamos en los cestos y consideramos los sucesos

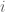A_i \equiv «la bola i cae en un cesto vacío» (para i=2,3)

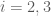vemos que calcular la probabilidad de que no haya eliminatoria entre dos equipos españoles es una pregunta que se puede responder con conocimientos básicos de probabilidad condicionada:

probabilidad-Champions

Actualización: podría decir aquello de «estaba preparado para ver si alguien prestaba atención», pero en absoluto, mi argumento está mal, sin paliativos. Un fiel seguidor del blog me lo ha hecho ver: el problema del modelo que propongo es que no excluye que haya tres bolas en un cesto, cosa prohibida en el sorteo. Eso sí, la solución que propone el lector (matemático, como yo) creo que tampoco es correcta. Al final, esta entrada va a ser sobre todo una prueba de que, con la probabilidad y la combinatoria, cualquiera puede cometer errores. Y que modelar de forma correcta es complicado, aún en situaciones «sencillas».

Como ya no me fío de nada he decidido recurrir a la «fuerza bruta», y contar las formas de colocar 3 bolas rojas en 4 cestos, sin permitir que haya 3 en el mismo. Son 16, y aquí están: 

sorteo-bolas-rojas

De esas 16, sólo en 4 se evita el emparejamiento entre dos equipos españoles. Por tanto, la probabilidad de que haya una eliminatoria española es 3/4. Nada extraño que haya ocurrido … 

Actualización 2: nuevo error, otra vez de principiante. Los sucesos de la figura NO son equiprobables. Si pensamos en las permutaciones de 8 elementos, que sí son equiprobables, y vemos el sorteo como emparejar 1 y 2, 3 y 4, etc, los sucesos con 3 bolas en distintos cestos se pueden completar a 8 permutaciones (en el sentido de contar sólo las posiciones de las bolas rojas), mientras que los que tienen dos bolas en un mismo cesto se pueden completar solo a 2. Visto así, el conteo para los sorteos sin emparejamiento español es 32/(32+56) = 4/7, que sí coincide con la solución que proponía Roberto Muñoz, el lector que me hizo ver mi primer error. 

Lo dicho, la probabilidad es resbaladiza, y si algún lector tiene un futbolín y cree que debo pasar por debajo de él, estoy dispuesto. 

Los currículos de la LOMCE

Espero que la salida del lío político en el que estamos incluya deshacerse de la LOMCE, y conseguir de una vez una ley educativa con consenso en los temas básicos, pero sobre todo espero que como parte de ese proceso podamos de una vez dedicarle un tiempo a los temas puramente educativos, a los currículos.

Con motivo de este curso de formación en Las Acacias estoy mirando un poco más en detalle el currículo de primaria de Madrid, y no lo voy a calificar por si esta entrada la leen menores …

@ClaraGrima y @lolamenting mencionaron en días pasados algunas erratas (no recuerdo si se trataba del currículo de Madrid o del currículo del Ministerio, tanto da). Eso ya es grave, pero es mucho peor el mensaje de fondo que transmite sobre qué son las matemáticas. Es difícil elegir el ejemplo más disparatado, pero me quedo con éste, sacado textualmente de los contenidos de 6º de Primaria, sobre proporcionalidad y porcentajes:

Usa la regla de tres en situaciones de proporcionalidad directa (ley del doble, triple, mitad …) para resolver problemas de la vida cotidiana.

Ya es grave que sigamos insistiendo con la regla de tres, cuando son sobradamente conocidos los problemas de aprendizaje que genera, y manteniéndonos como uno de los poquísimos países donde se sigue usando, pero es peor todavía eso de «ley del doble, triple, mitad». La verdad, no las había oído nunca, pero en este contexto sólo pueden referirse a que si compro el doble de cierto producto, pago el doble, y si compro la mitad, pago la mitad. ¿De verdad eso es una ley, y tiene que acabar con el correspondiente recuadro amarillo en el libro de texto? Ni siquiera suena a siglo XX, ¡más bien a siglo XIX!

El máximo común divisor

El pasado sábado hubo una interesante conversación en twitter alrededor del máximo común divisor y los algoritmos para calcularlo. @druizaguilera proponía este diagrama conjuntista para determinar los factores comunes: mcd-conjuntos

@raulf aportó este otro enfoque:

mcd-cuadraditos

 

todo empezó con este tuit del pasado 7 de febrero: https://twitter.com/dacilgonz/status/696336412078186498

Estos días he seguido dándole vueltas al tema, y han cristalizado algunas ideas sobre las que llevaba tiempo pensando.

El primer comentario es que los métodos propuestos son realmente algoritmos para calcular intersecciones de multiconjuntos, y mi gran pega es que enseñan muy poco sobre qué es el máximo común divisor. Mi impresión es que la mayor dificultad de este tema no es el cálculo, sino la comprensión del concepto, para poder aplicarlo en la resolución de problemas. Del vídeo que enlacé en su día sobre lo que hacían mal en Singapur en los años 70, me interesa cada vez más una de las cosas que se mencionan: los procedimientos y la comprensión conceptual hay que trabajarlos en paralelo (el vídeo dura 5 min, y este tema se empieza a tratar a los 40 seg):

Para trabajar en paralelo la comprensión y el cálculo del mcd (y del mcm) me parece más interesantes las actividades que proponen Cecilia Calvo y David Barba en su trabajo publicado en SUMA, y que los autores han puesto aquí (vía @druizaguilera).

El tema del máximo común divisor y el mínimo común múltiplo lo trato en magisterio, a todos los alumnos les suena la receta de «factores comunes …», y lo hacen bien, en general, sin necesidad de procedimientos ad hoc. Lo que me sorprende es que ninguno parece estar familiarizado con el hecho de que a partir de la factorización de un entero es fácil escribir el conjunto de sus divisores, lo cual es tanto como decir que no tienen idea de por qué funciona la receta que usan para calcular el máximo común divisor. Creo que es un tema sencillo de entender, no hay más que pararse a comparar el conjunto de divisores de un número como 36 con su factorización. La relación entre factorización y divisores da mucho juego (estos temas han sido para mí un descubrimiento reciente, a raíz de impartir clases en magisterio: la aritmética elemental está llena de relaciones que dan lugar a auténtico pensamiento matemático). Por ejemplo, a partir de la relación entre factorización y divisores se pueden contar el número de divisores de un entero: si n = p^2\cdot q^3\cdot r (p, q y r son números primos distintos, claro), entonces n tiene 24 divisores. A la inversa (examinar un problema al revés es una de las mejores formas de profundizar en su comprensión), puedo construir números con, por ejemplo, 18 divisores, de estas formas: p^8\cdot q, $p^5\cdot q^2$, p^2\cdot q^2 \cdot r. ¿Cuál es el número más pequeño que tiene 18 divisores?

Hay otro aspecto quizá incluso más importante. Los pedagogos dicen (y en este punto estoy de acuerdo con ellos) que algo se ha aprendido de verdad cuando el conocimiento se puede transferir a otra situación. Y aquí radica la extraordinaria potencia del método matemático: que las ideas y las estrategias que involucra son transferibles a una cantidad sencillamente sorprendente de situaciones. Cuanto más especializado sea un procedimiento, menos transferible será. No dudo de que las propuestas del principio de esta entrada sean útiles para que los alumnos hagan los cálculos necesarios para superar el examen correspondiente, lo que dudo es qué quedará de todo eso un año después de haber hecho ese examen.